S rozvojem stavební činnosti se zvyšují požadavky na kvalitu a využívání nových typů těsnicích materiálů. Těsnění konstrukčních spár musí zachycovat a přenášet mechanická, chemická a tepelná namáhání při vystavení nepříznivým účinkům působení světla, kyslíku, ozonu, agresivních oxidů, vlhkosti, které urychlují jejich stárnutí.
Teoretická část
Namáhání a deformace výplně spár
Typy a velikost spár, do kterých se těsnicí tmely různým způsobem nanášejí, jsou velmi rozmanité. Nejpodstatnějším vlivem, který zde působí, jsou tepelné objemové změny těsněných materiálů.
Pro určení namáhání, případně deformací výplně spár je potřeba znát:
a) charakter deformace prvků vzájemně propojených,
b) velikost dilatačního pohybu,
c) vliv tvaru spáry, druhu těsniva a struktury prvků na řešení koncepce spoje.
Charakter deformace prvků
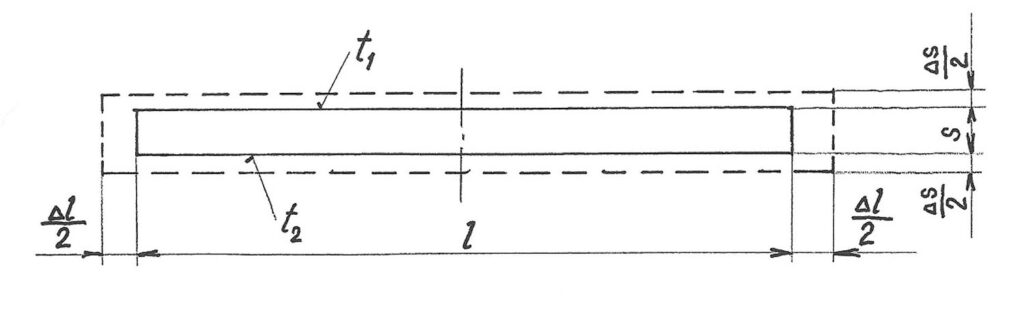
Při deformaci se vyskytují změny objemu a tvaru. Na obr. 1 je znázorněna změna objemu při rovnoměrném oteplení prvku (t1 = t2).
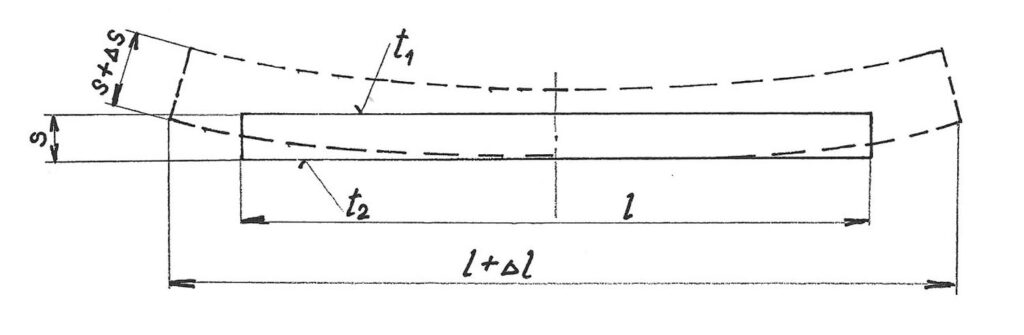
Při nerovnoměrném oteplení se při změně objemu prvku mění i jeho tvar(t1 <t2), jak je patrno z obr. 2.
Toto rozlišení charakteru deformace má praktický význam, poněvadž umožňuje charakterizovat změny vyskytující se porůznu u jednotlivých prvků stavby. Pokud jsou prvky tvaru tyče nebo tenkostěnné desky, rozhodují změny základních délek, a to v jednom ze základních směrů. Malý rozměr je nepodstatný.
Tuto problematiku je nutno doplnit o další skutečnost. Je známo, že každé homogenní těleso izotropní, lineárně a ideálně pružné mění vlivem rozměrových změn svůj objem, případně tvar.
Důležité však je, že každé těleso po dosažení své homogennosti charakterizované požadovaným modulem pružnosti je tedy ve stavu, který můžeme nazvat stabilizací prvku (tj. např. beton po 28 dnech). Od tohoto stavu je možné teprve pozorovat zkrácení či prodloužení prvku.
K tomu, abychom mohli správně hodnotit průběh a charakter cyklických objemových změn vyvolaných změnou teploty, je nutné deformace prvků rozdělit na:
1. deformace počáteční (dočasné),
2. deformace trvalé (cyklické).
Počáteční deformace prvků (jednovrstvých)
Kolísání změny objemu v tomto případě je přímo úměrné kolísání teploty vnějšího prostředí. Tento proces nevzniká najednou, ale závisí na horní hranici teplotní jímavosti materiálu prvku v závislosti na čase. Například, je-li stabilizovaný prvek uložen dlouhodobě do prostředí s vyšší nebo nižší rovnoměrnou teplotou, snaží se dosáhnout – naakumulovat parametry prostředí. Tím se dočasně dostává do současného stavu napjatosti, případně se deformuje při současné změně objemu.
V těch případech, kdy je prvek trvale deformován nerovnoměrnou povrchovou teplotou a je vložen do prostředí s dlouhodobou rovnoměrnou teplotou, nemění sice svůj objem, ale projevuje se postupně změnou tvaru.
Deformace trvalé, cyklické
Tepelné objemové změny jsou základní příčinou deformace stavby a jejich jednotlivých částí. Je všeobecně známo, že každé homogenní těleso mění svůj objem úměrně s teplotou. Předmětem dalšího rozboru bude spoj uměle vytvořený v takovém tělese. Jedná se o prostou přímou spáru, která je vyplněna těsnicí hmotou (tmelem). Je zřejmé, že tento materiál bude podle velikosti a směru pohybu obou stavebních dílců namáhán dosti složitým způsobem. Může se jednat jak o jednoduchý tah či tlak, tak i o prostý smyk, ale s největší pravděpodobností to budou kombinace těchto způsobů namáhání, které se uplatní nejvíce v počátečním období dokončení stavby a v dalším čase ustupují. V této době se nejvíce budou uplatňovat již pouze deformace způsobující namáhání těsnicí hmoty na tah nebo tlak. Z hlediska absolutní hodnoty tahové deformace bude u tohoto typu spáry kritická zejména její šířka, tj. velikost směru „s“, respektive poměr s/h (obr. 3).
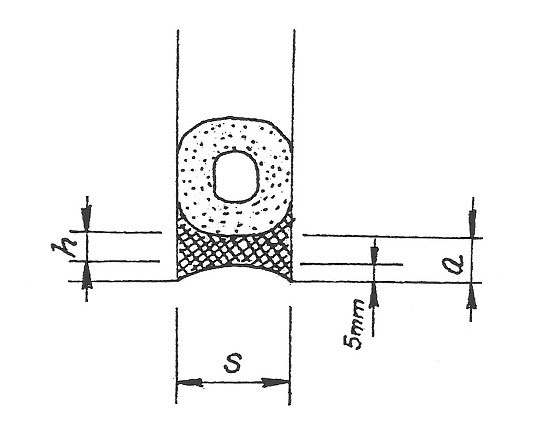
Převážná část deformací se tedy bude koncentrovat ve směru šířky spáry. Tato šířka může být v praxi velmi rozmanitá. Z hlediska deformace těsnicího tmelu bude situace tím příznivější, čím větší tento rozměr bude. Toto však všeobecně nelze zajistit, neboť z funkčního hlediska by měla šířka spár být v mezích navržených tolerancí daného objektu. Na základě těchto skutečností je snaha deformaci tmeleného profilu příznivě ovlivnit jeho geometrickým tvarem, tj. vytvořením bikonkávního tvaru jeho průřezu (viz obr. 3).
Pro tmely elastické a elastické s plastickým podílem je nutno respektovat vztah mezi h a s:
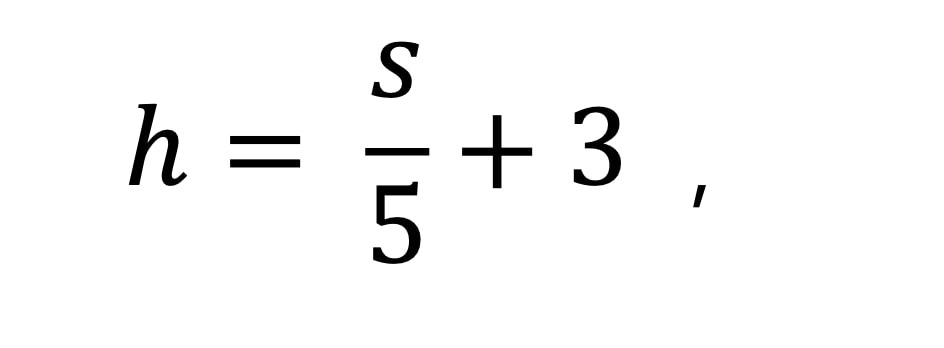
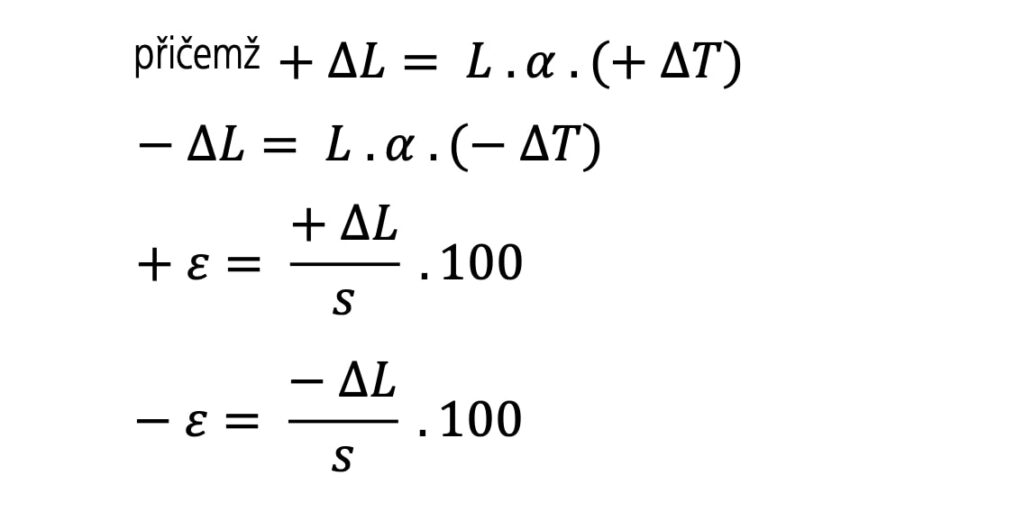
kde jsou s šířka spáry při tmelení a h minimální tloušťka tmelu ve spáře.
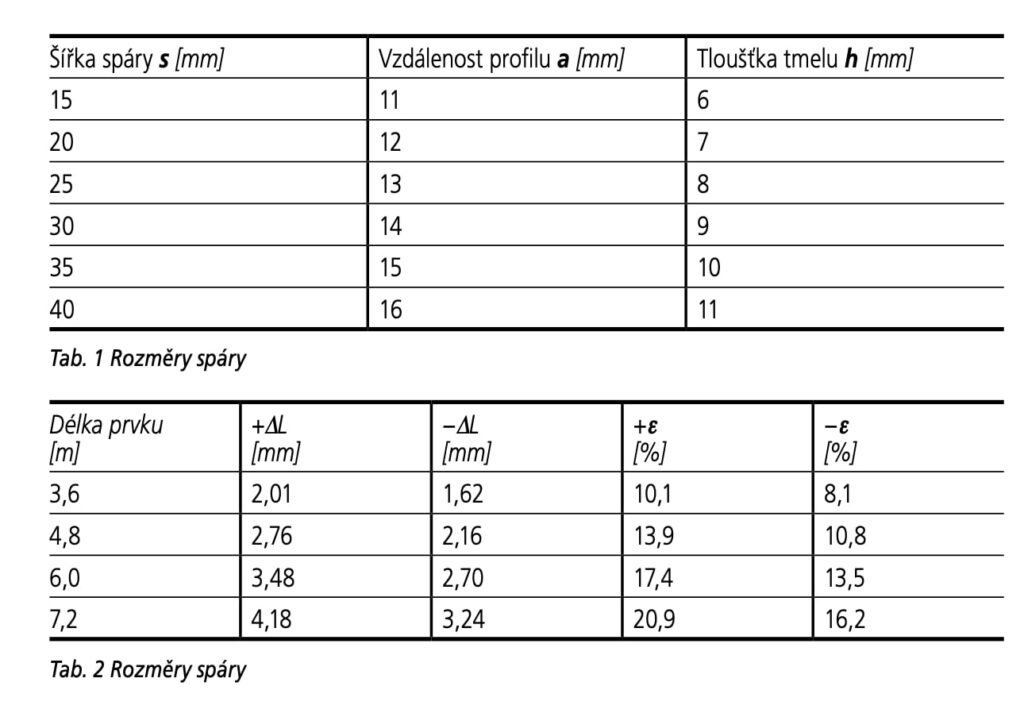
Tabulka 1 pak udává jednotlivé hodnoty h a a (a – hloubka zatlačení pokladního profilu) pro některé možné šířky spáry.
Deformace těsnicích tmelů aplikovaných do vnějších spár budou dány rozměrovými změnami šířek spár, což ovlivňuje dilatace stavebního prvku vlivem teploty. Při teoretických výpočtech se běžně používá hodnota koeficientu délkové teplotní roztažnosti α = 10∙10-6 [°C-1] pro betonové prvky s tím, že se uvažuje prvek dilatačně volný se zanedbáním vlastní tíže. Při projektové šířce spáry např. s = 20 mm a uvažovaných okrajových teplotách Tmin = −18 °C a Tmax = +50 °C je možno teoreticky vypočítat příslušné poměrné deformace ε. Pro elastické tmely nebo tmely elastické s plastickým podílem se absolutní hodnota ε skládá z míry namáhání v tahu i tlaku. V tomto případě se při výpočtu bere do úvahy teplotní hranice, ve které může být tmel nanášen. Pohybuje se běžně mezi spodní hranicí, tj. +5 °C, a horní hranicí +40 °C.
Při zpracování, které probíhá na spodní hranici, tedy při +5 °C, dosahují maximální teplotní rozdíly: pro protažení … od +5 °C až do −18 °C, tj. 23 °C, pro stlačení … od +5 °C až do +50 °C, tj. 45 °C. Pro horní hranici, tedy při +40 °C, platí: pro protažení … od +40 °C až do −18 °C, tj. 58 °C, pro stlačení … od +40 °C až do +50 °C, tj. 10 °C.
Rozhodující teplotní rozdíly, kterým může být těsnicí materiál v extrémním případě vystaven, jsou pro protažení 58 °C a pro stlačení 45 °C.
Pro železobetonové prvky různých délek udává přehled o příslušných nejnepříznivějších teoretických deformacích tabulka 2.
Podle uvedených teoretických výpočtů je zřejmé, že např. u prvku délky 7,2 m bude nejnepříznivější tahová deformace (pro s = 20 mm) pro elastický tmel +20,9 % a nejpříznivější +8,3 %. Tyto teoretické hodnoty jsou značně vysoké a zřejmě v praxi budou deformace menší. O praktických jejich hodnotách bude pojednáno v experimentální části.
Rozbor poměrů při relaxaci napětí ve tmelech
Ve skutečných podmínkách, při kterých má těsnicí tmel vykonávat svoji funkci, se bude jednat vždy o dlouhodobé působení všech vnějších faktorů. Rychlosti deformačních změn jsou až na výjimečné případy velmi malé. Z toho důvodu lze předpokládat, že u elasticko-plastických tmelů bude rozhodující jejich časové přizpůsobení patřičným deformacím. To znamená, že je potřeba upravit jejich vlastnosti z hlediska příznivého průběhu relaxace napětí.
Stanovení deformačních charakteristik spárových těsnicích tmelů vychází ve své podstatě ze sledování poklesu napětí vzorku tmelu zatěžovaného definovaným způsobem. Pro tuto zkoušku je tmel fixován ke vhodným kontaktním materiálům takovým způsobem, že zkušební těleso má tvar kvádru o rozměru 50 × 12 × 12 mm (ČSN EN ISO 11600). Zkušební vzorek tmelu se protahuje ryhlostí 5,5 ± 0,7 mm/min o 18 mm, tj. na hodnotu protažení ε = 150 %. Napětí ve vzorku vyvolané touto deformací se nechá 20 minut relaxovat a po skončení zkoušky se vypočítá poměr sil
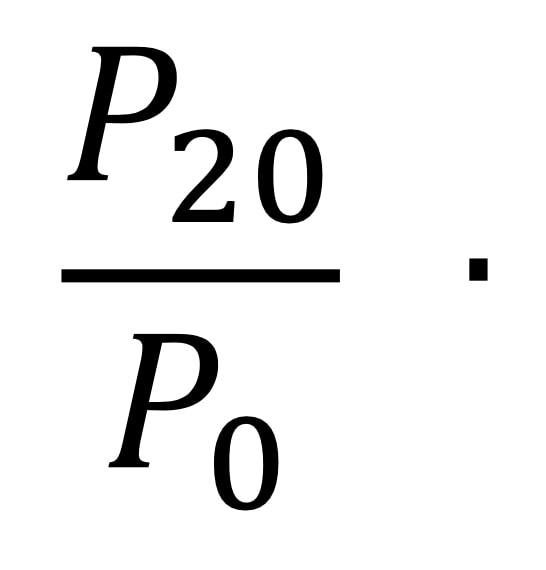
V případě, že tato hodnota leží v intervalu 0,8 až 1,0, označíme tmel jako elastický. Při poměru sil 0,2 až 0,8 se tmel považuje za elastický s plastickým
V případě, že tato hodnota leží v intervalu 0,8 až 1,0, označíme tmel jako elastický. Při poměru sil 0,2 až 0,8 se tmel považuje za elastický s plastickým podílem. Je-li poměr sil menší než 0,2, jedná se o tmel plastický.
Časovou závislost síly v průběhu celé zkoušky za předpokladu jejího lineárního nárůstu i poklesu je možno sledovat na obr. 4. Z obrázku jsou okamžitě zřejmé vztahy mezi silami na konci zkoušky pro jednotlivé typy těsnících tmelů.
V případě reálného viskoelastického tělesa je schéma znázorněné na obr. 4 jen velmi hrubým přiblížením ke skutečným poměrům při zkoušce. Nárůst síly při zatěžování při konstantní deformační rychlosti bude mít pro většinu polymerních materiálů do poměrné deformace 150 % parabolický průběh konvexního tvaru. Na druhé straně při relaxaci napětí po dosažení konečné deformace bude mít pokles síly téměř exponenciální charakter.
Matematický popis celého průběhu zkoušky je značně komplikovaný, zejména s ohledem na její první fázi, kdy se zkušební vzorek zatěžuje. Analýza celého problému se zjednoduší, uvážíme-li skokový nárůst síly P0 na její maximální hodnotu v čase t = 0. V takovém případě se jedná o klasický případ relaxace napětí.
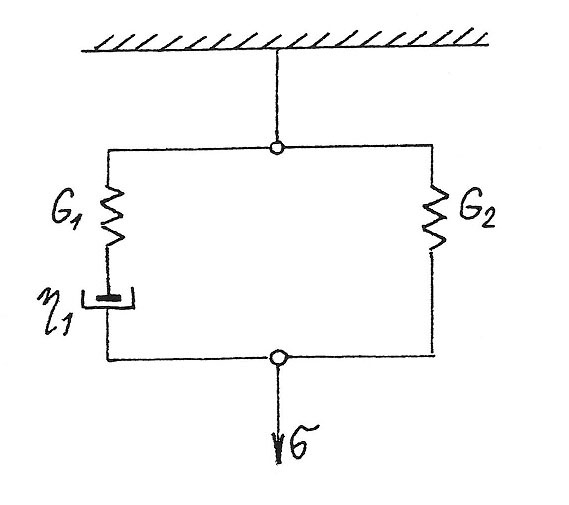
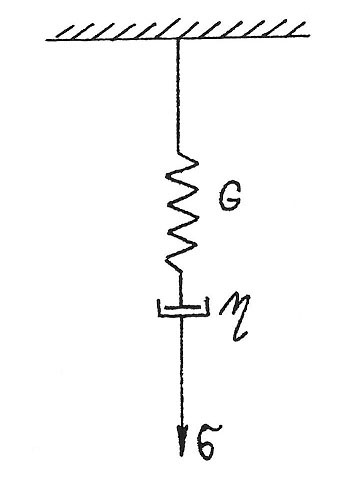
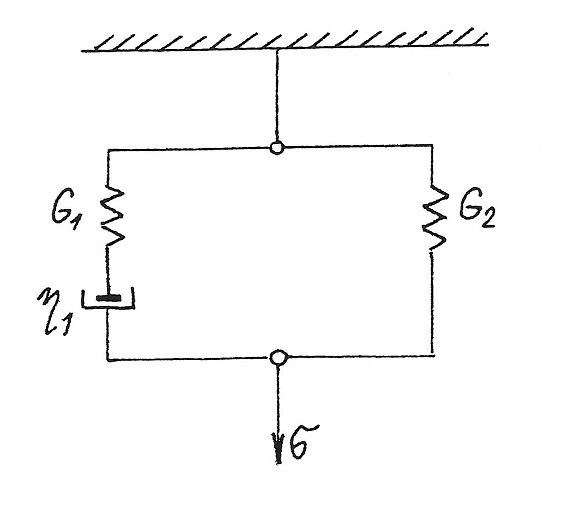
Relaxaci napětí viskoelastického tělesa je možné velmi lehce znázornit pomocí Maxwellova modelu tvořeného pružinou a netěsným pístem, pohybujícím se ve válci naplněném viskózní kapalinou, jak je znázorněno na obr. 5.
Hodnoty G a η jsou konstantní (G – smykový modul; η – viskozita). Zatížíme-li model napětím σ budou deformace jednotlivých elementů modelu
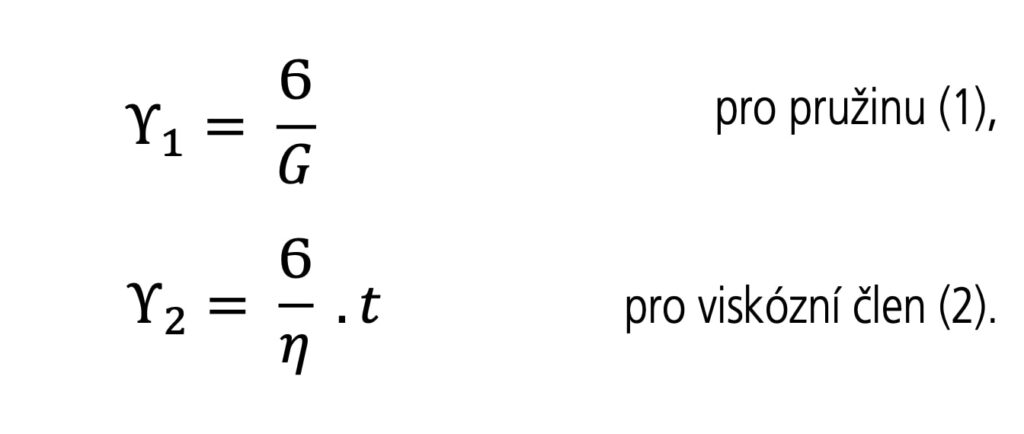
Celková rychlost deformace Maxwellova modelu Y˙c potom je:
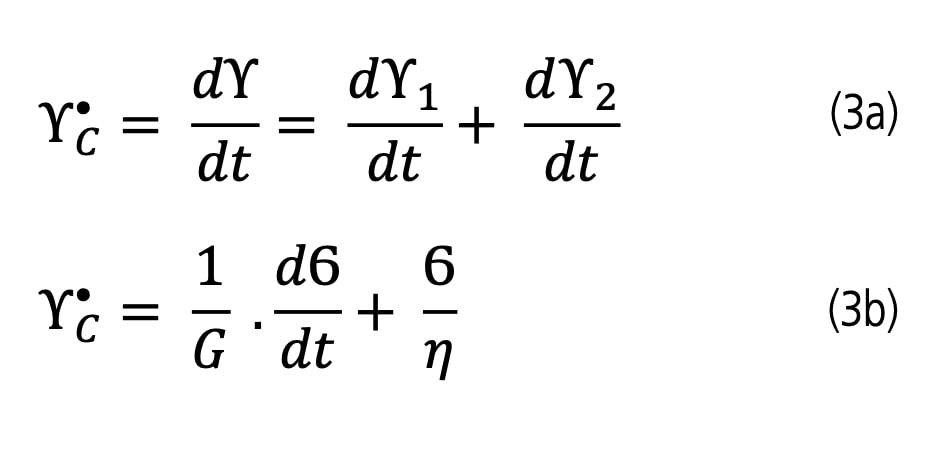
Při relaxaci napětí je deformace modelu konstantní, tj.

Separací proměnných pak získáme konečný vztah:
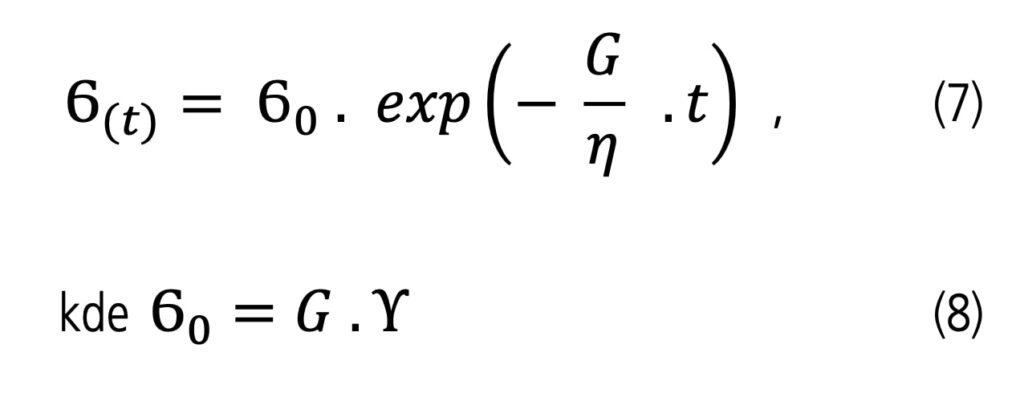
je počáteční napětí v čase t = 0
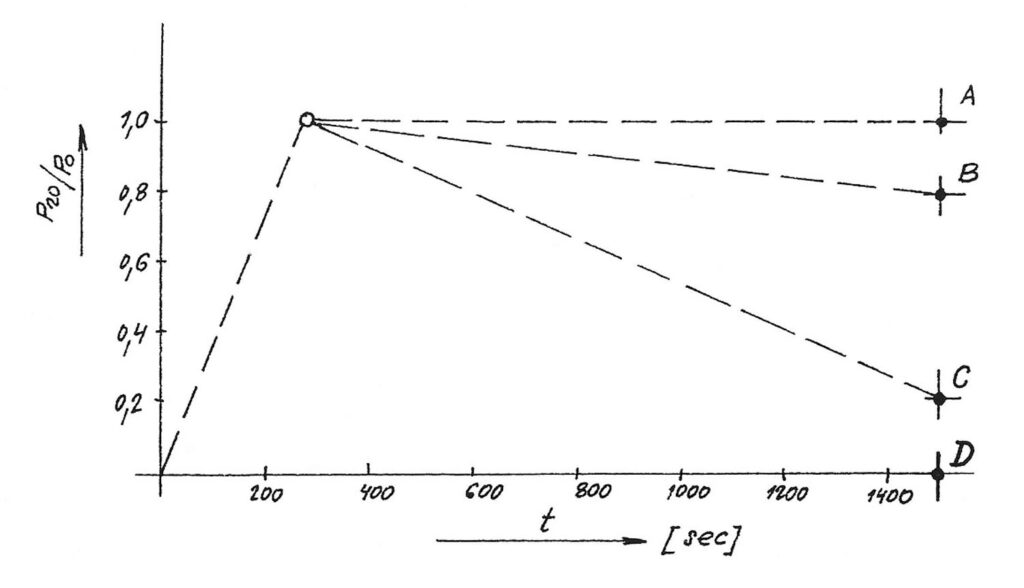
Aplikujeme nyní rovnici (7) pro případ relaxace napětí viskoelastického tělesa pro jednotlivé body A, B, C, D znázorněné na obr. 4. Relaxační čas τ=η/G stanovíme ze vztahu:
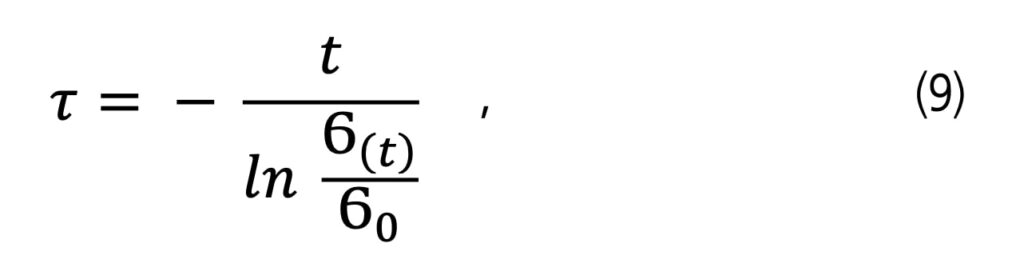
potom v bodě:
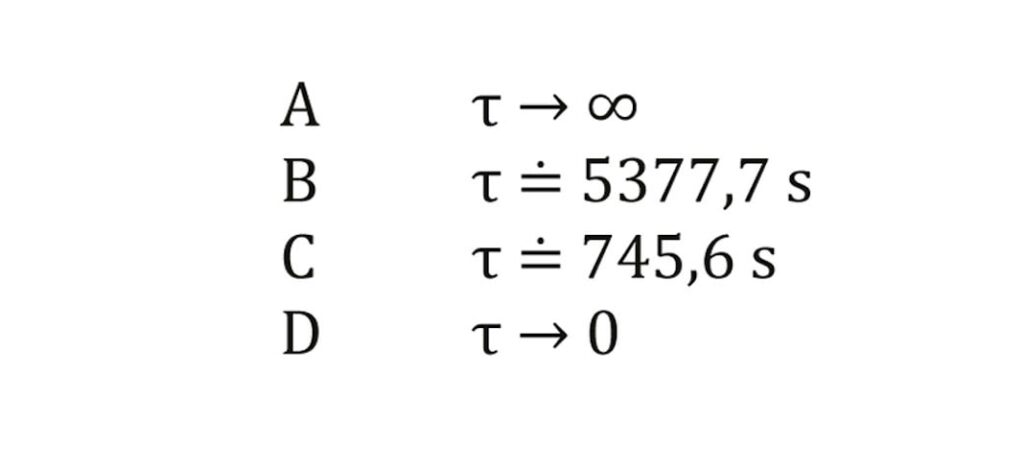
Názornou představu o změně síly v závislosti na čase pro klasický případ relaxace Maxwellova modelu při výše uvedených časech vidíme z obr. 6.
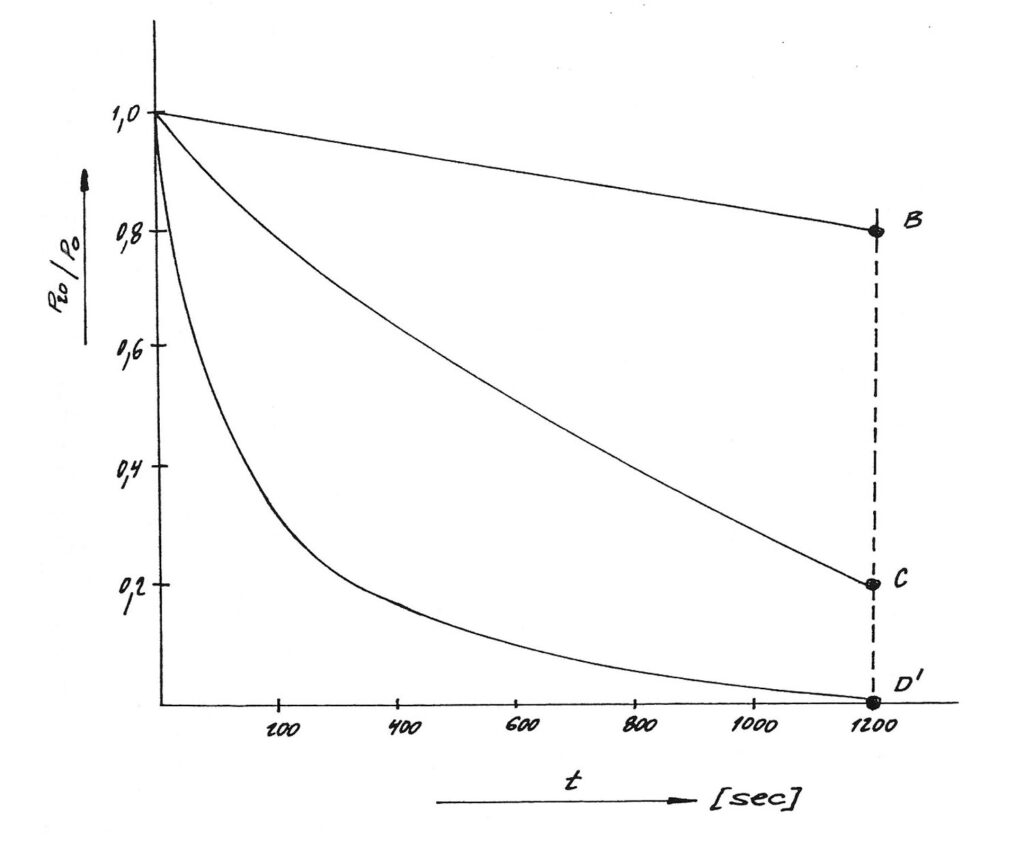
Maxwellův model charakterizuje chování jednoduchého lineárního polymeru. Elastické spárové tmely však mají ve většině případů trojrozměrnou polymerní strukturu, tj. jsou tvořeny více i méně dokonalou sítí. Relaxační chování takového polymeru proto musíme modelovat složitějším modelem, než je Maxwellův. Pro jednoduchost použijeme tzv. model Kuhnův, který je tvořen dvěma paralelně spojenými modely Maxwellovými. Aby model vykazoval chování obdobné síťovaným polymerům, zvolíme viskozitu η2 extrémně vysokou. V tomto případě (η2→∞) lze uvedený element z modelu vyloučit a obdržíme tak tříparametrový model znázorněný na obr. 7.
Při deformaci tohoto modelu vlivem napětí σ bude platit:

ale napětí σ se rozdělí do dvou složek

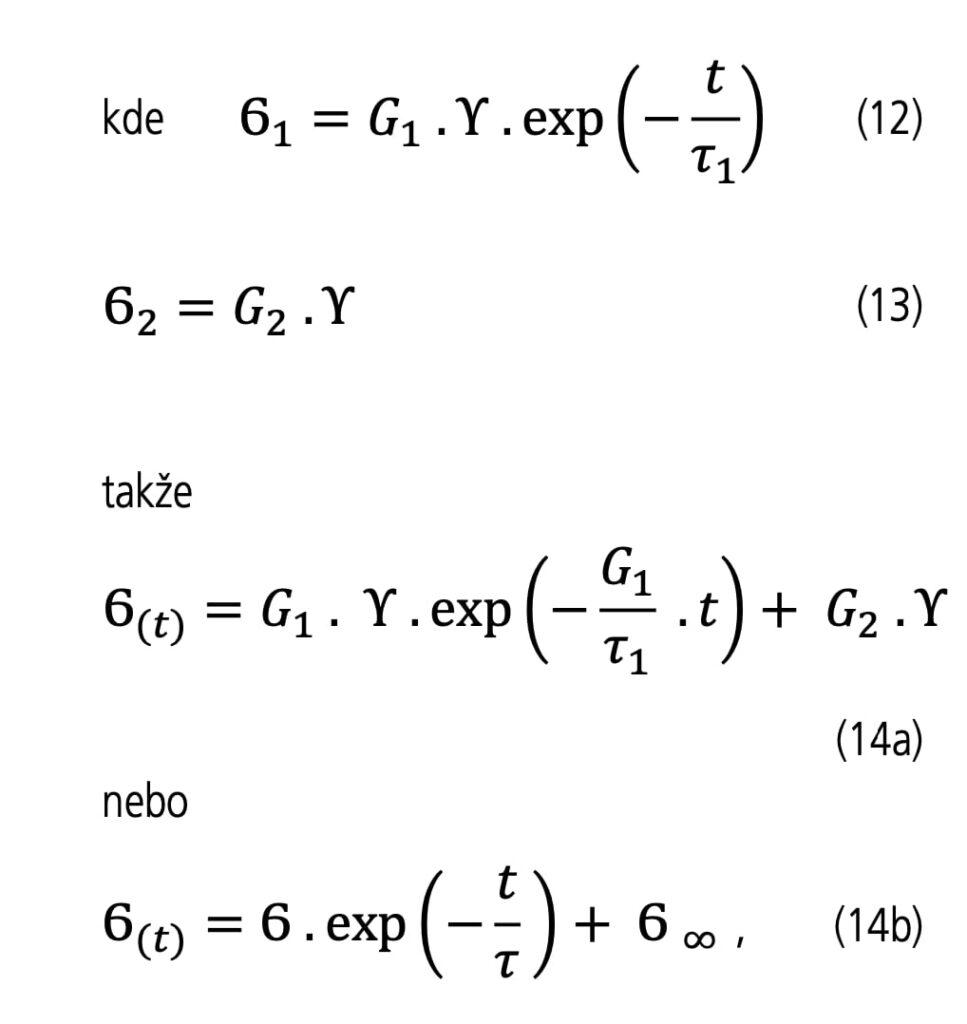
kde σ∞ je rovnovážné napětí u tohoto modelu po nekonečně dlouhém čase.
Uvažujeme-li opět klasickou relaxaci napětí, potom předpokládejme, že v bodech B a C bude model v rovnovážném stavu. Potom pro bod B bude platit σ = 0,2; σ∞= 0,8 a pro bod C σ= 0,8; σ∞= 0,2.
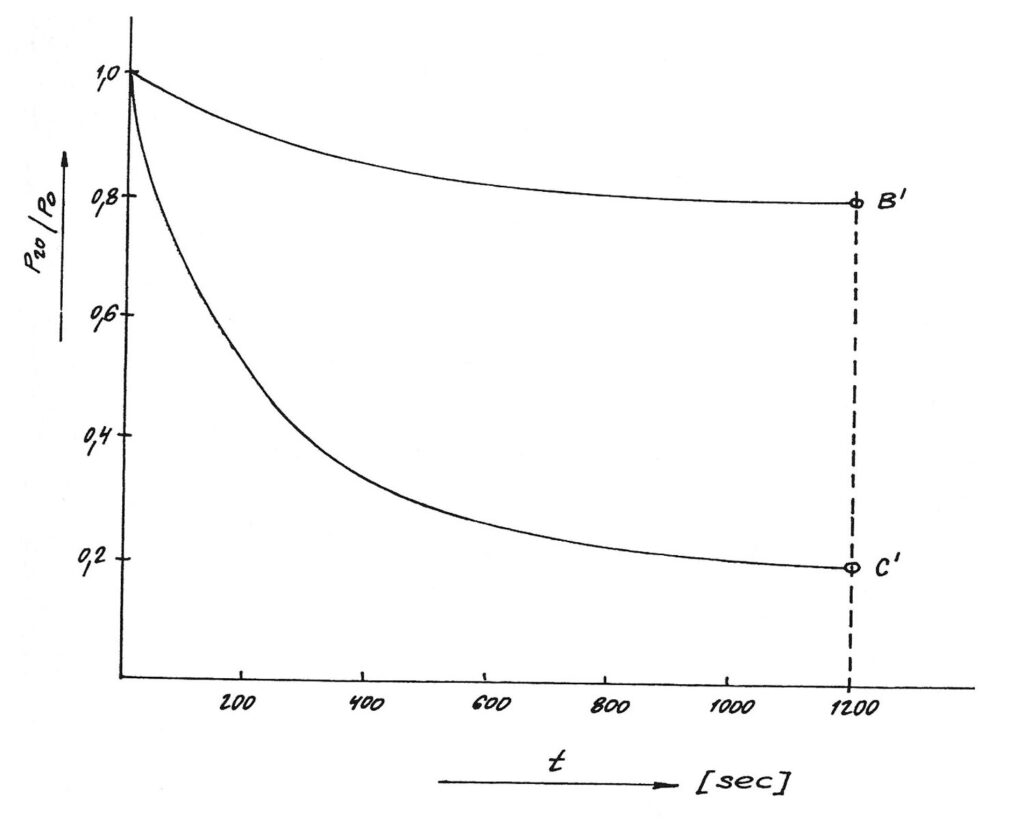
Pro stanovení hodnot relaxačních časů však musíme z čistě matematického hlediska předpokládat přiblížení na 0,1 %, potom pro oba limitní body B‘ a C‘ bude mít relaxační čas hodnoty:
bod B‘ τ= 225,5 s,
bod C‘ τ= 179,5 s.
Průběh relaxace tohoto modelu je znázorněn na obr. 8.
Porovnáme-li nyní mezi sebou hodnoty relaxačních časů pro dané mechanické modely v bodech B, B‘, C, C‘, zjistíme, že u modelu sítovaného polymeru jsou relaxační časy značně kratší. Z jednoduchého úsudku potom vyplývá, že při uvažování výše uvedených jednoduchých modelů lze jejich chování označit jako plastické vady, platí-li, že τ< 179,5 s. Chování jednoduchého modelu bude elastické, bude-li relaxační čas mít hodnotu τ> 5377,7 s.
Pro Maxwellův model je modul pružnosti:
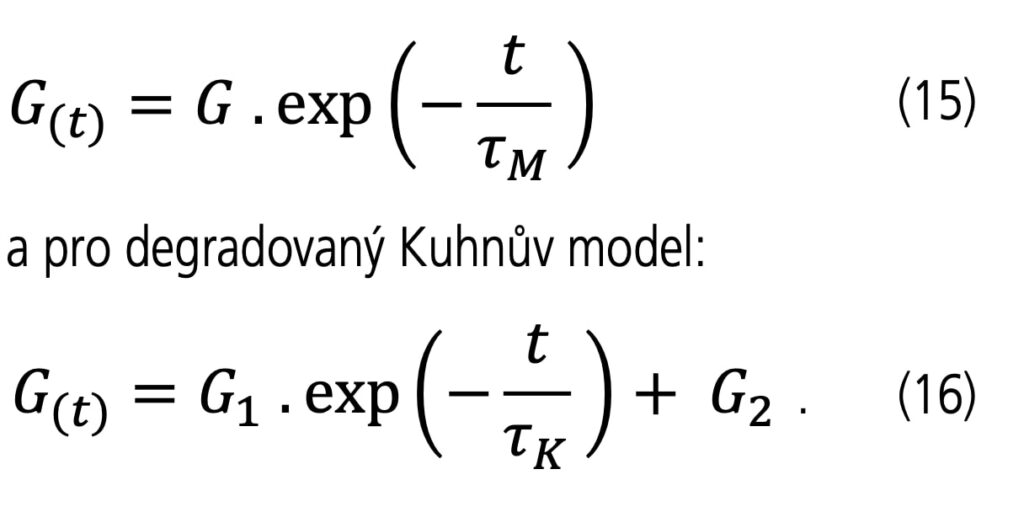
Experimentální část
Praktické hodnoty deformací
Na základě dřívějšího výzkumu dilatačních vnějších spár panelových budov se ze zkoušek odolnosti tmelů vůči střídavému mechanickému namáhání (tah – tlak) odvozovala hodnota tzv. praktické tažnosti, kterou může být tmel namáhán po dobu jeho životnosti. Bylo stanoveno, že tato hodnota vzhledem k materiálové skladbě tmelů nepřekročí 20 %.
Dilatace betonových prvků u různých staveb ovlivňují přímo spárový systém a vyvolávají v těsnícím tmelu tahová namáhání. Experimentální základna výzkumu stavebních prvků při VÚPS Praha provedla již dříve řadu měření za účelem zjištění skutečného koeficientu délkové roztažnosti αexp u různých panelových staveb.
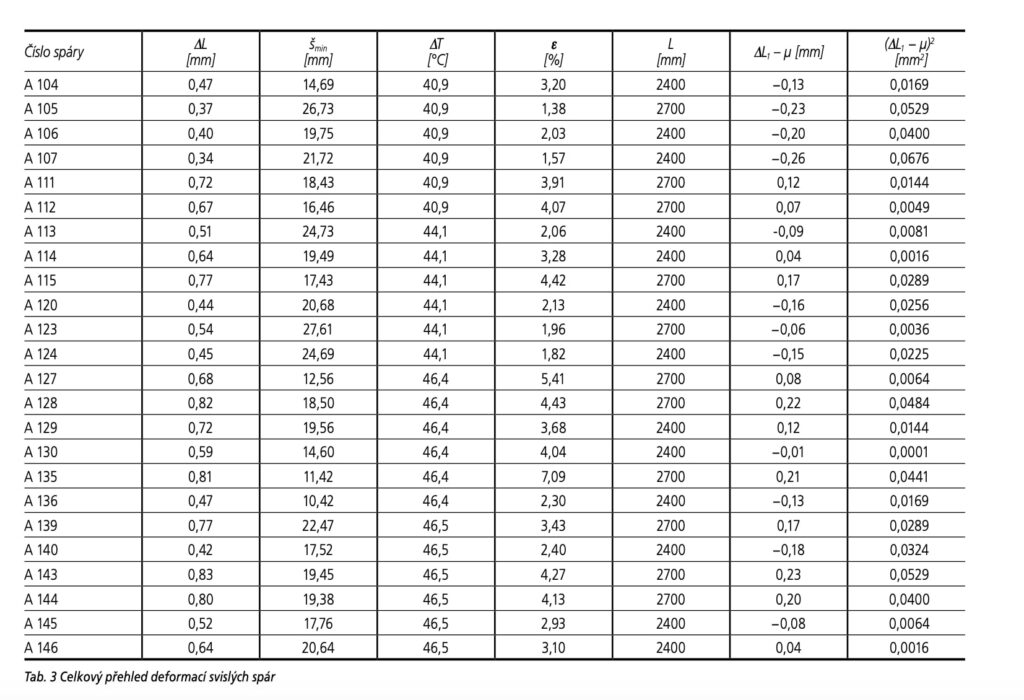
Při zjišťování deformací vrstvených dílců se vycházelo z měření prováděného na západním štítě objektu. Maximální možné αexp bylo odvozeno z rozměrové změny svislé spáry ΔLmax= 0,83 mm a činilo 6,6⋅10−6 (°C−1), viz tabulka 3.
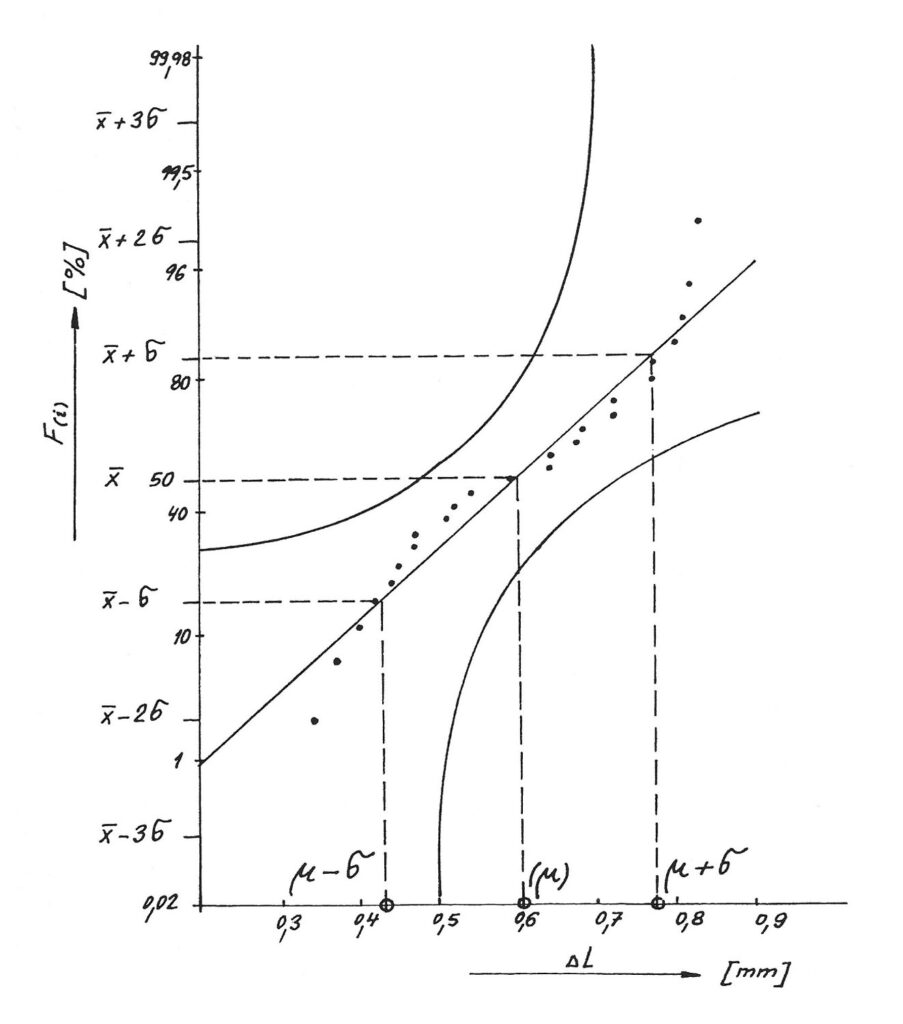
Z náhodného výběru svislých spár (n = 24), kde ΔLmin= 0,34 mm a ΔLmax= 0,83 mm byl proveden statistický rozbor deformací. Grafickou metodou (obr. 9) bylo potvrzeno, že pro rozměrové změny platí zákon normálního (Gaussova) rozdělení.
Průměrná změna šířky spáry μ byla:
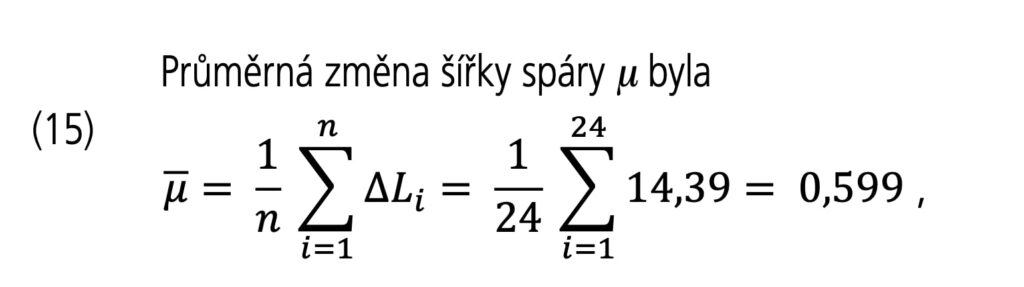
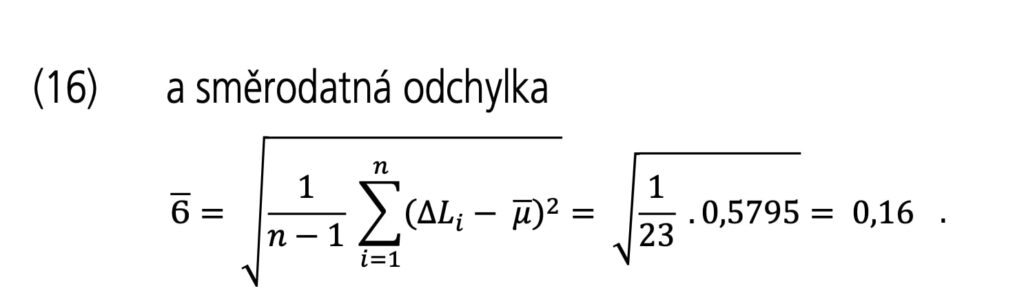
Při projektové šířce spáry 20 mm a toleranci ±2 mm byl tmel v její nejmenší montážní šířce namáhán v rozmezí 2 až 4,6 %. Tak například v případě spár mezi silikátovými dílci, kde αteor= 10⋅10−6 mm/mm °C a maximální rozdíl zimní a letní teploty Δt= 60 °C, chceme určit minimální šířku spáry v případě, že se použijí stavební dílce o délce 6 m a utěsnění spár tmel s dlouhodobou trvalou deformací 20 %. Změna délky stavebního dílce ΔL se bude rovnat:
ΔL= α⋅L⋅Δt = 10⋅10−6⋅6000⋅60= 3,6 mm
Minimální šířka spáry se pak stanoví ze vzorce:
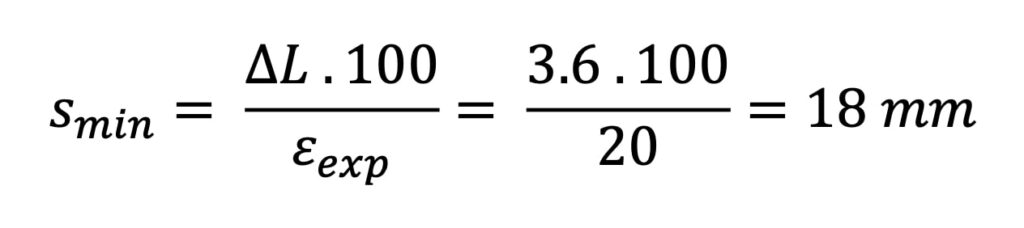
Pokud by šířka spáry při montáži činila např. 10 mm, tak tmel by byl nucen přenášet dlouhodobé deformaci 36 %, což by zřejmě vedlo k závadám. Na základě získaných znalostí o deformacích betonových prvků jsme mohli přikročit k vývoji těsnící hmoty, která materiálově (čili chemicky) i fyzikálně (přenosem deformací) bude dlouhodobě utěsňovat dilatační spáry.
Vývoj elasto-plastického těsnícího tmelu
Vzhledem k tomu, že každý nový těsnící materiál má kromě výhodných těsnících vlastností i některé z technického nebo ekonomického hlediska nevýhodné parametry, je třeba při perspektivních úvahách o přínosu pro stavebnictví posuzovat tyto materiály komplexně.
Akryláty byly v dřívější době používány převážně jako výplňové systémy pro vnitřní spáry. Dnes, kdy sortiment výroby disperzí pro akrylátové tmely je značně široký (společnost BASF Ludwigshafen) a vykazuje kvalitní parametry, lze formulovat i receptury tmelů do vnějších spár.
Jde hlavně o kopolymerní disperze s roztokovými polymery obsahující akrylátovou složku, které působí v molekule polymeru jako vnitřní plastifikátor a dávají jinak dříve tvrdým a neohebným filmům vhodné aplikační i užitné vlastnosti.
Nejčastější druhy disperzí a roztokové polymery používané pro výrobu tmelů lze rozdělit do těchto skupin:
- akrylátové kopolymery (kombinace styren nebo vinylacetát),
- roztokové kopolymery,
- estery kyseliny akrylové.
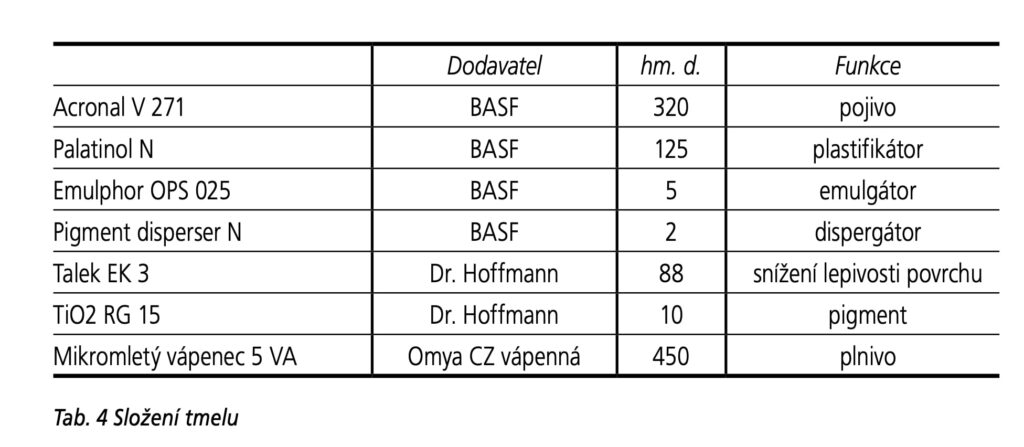
Pro vyvíjený tmel byla zvolena vodná disperze polymeru na bázi esteru kyseliny akrylové s akrylonitrilem. Na základě přípravy velké řady laboratorních směsí a po odzkoušení nutných parametrů bylo možno formulovat tuto recepturu (viz tabulka 4).
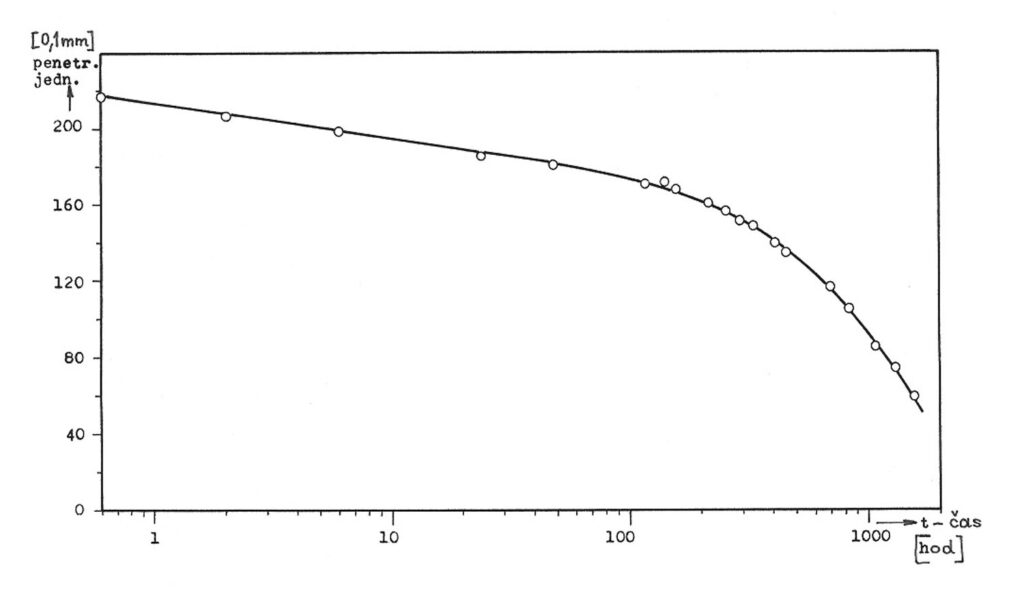
Průběh síťování u různých směsí byl sledován penetrační zkouškou (obr. 10).
Ukázalo se, že ve většině případů dochází při poklesu penetrací na hodnotu cca 100 penetračních jednotek ke znatelné změně vlastností, kdy u tmelů se začínají výrazně projevovat charakteristické vlastnosti elastických hmot.
Základní fyzikálně-mechanické vlastnosti jsou uvedeny v tabulce 5.
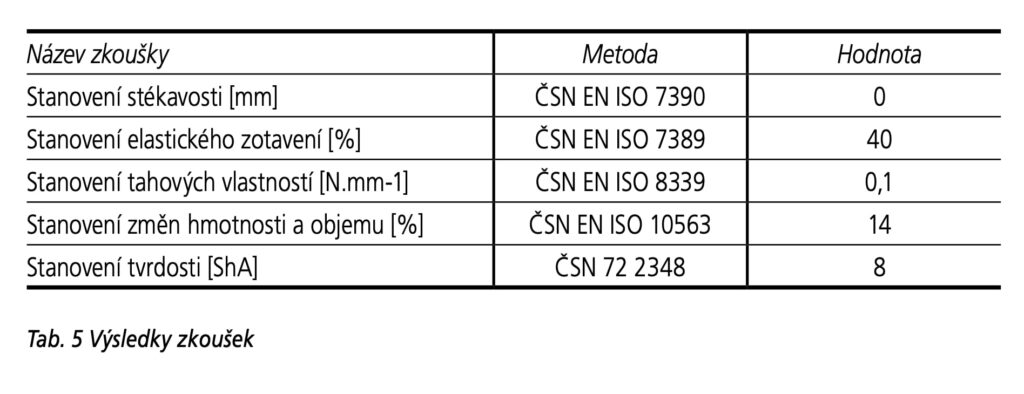
Tahové diagramy prokazují, že akrylátový tmel je nízkomodulového typu. Porovnáním tahových diagramů v oblasti předpokládaného dlouhodobého deformačního namáhání (+12,5 až 20 %) je zřejmé, že vyvinutý tmel má hodnotu odpovídajícího modulu výrazně nižší, což je příznivý parametr vzhledem k namáhání betonových ostění v praxi, zvláště když zkušební rychlost je řádově 5 až 6·10⁴ větší než skutečná rychlost dilatačních změn betonových prvků.
Na základě provedených zkoušek předepsaných pro konstrukční tmely v normě ČSN EN ISO 11600, lze tento tmel označit jako těsnící hmotu F 12,5 ÷ 20 E.
ADOLF MUSIL, PETR MITÁČEK
Ing. Adolf Musil ( 1945)*
Po maturitě na střední průmyslové škole strojírenské ve Zlíně vystudoval na VUT Brno, Fakultě technologické obor syntetických polymerů. V roce 1970 nastoupil do VÚPS Praha na pozici odborného asistenta vývoje polymerních a elastomerních těsnicích materiálů. Během působení v této společnosti obdržel řadu patentů. V roce 1982 jako člen JZD Slušovice řídil výstavbu biotechnologických laboratoří a provozů a později zástupce ředitele. Je autorem knihy „Spárové těsnící tmely ve stavebnictví“, kterou v r. 1985 vydala SNTL Praha. Od r. 1991 samostatně podniká jako OSVČ ve výzkumu a vývoji lepících a těsnicích směsí včetně betonových s využitím bioremediace.
Ing. Petr Mitáček ( 1972)*
vystudoval Technickou univerzitu ve Zvolene, Fakulta dřevařská. V současné době pracuje pro Mendelovu univerzitu v Brně ve Zkušebně stavebně truhlářských výrobků ve Zlíně v oblasti posuzování shody a certifikace.
Publikováno v časopise Materiály pro stavbu 2/2024
Literatura
Voldřich, F.: Problematika spár a spojů montovaných staveb. In: Těsnění kar montovaných staveb. Vysoké Tatry 1974, kap. I
Holzmüller, W., Altenburg, K.: Fyzika polymerů. Praha, SNTL 1966
Musil A., Pejchal L. J.: Spárové těsnící tmely ve stavebnictví. Praha, SNTL 1985
Reisenauer, R.: Metody matematické statistiky. Praha, SNTL 1970
Musil, A. & kol.: Geometry of characteristic joints. Holztechnologie, r. 52, č. 4/2011
Del Giudice, F., J. Haward, S., Q. Shen, A.: Relaxation time of dilute polymer solutions: A microfluidic approach. Journal of Rheology 61, 327, 2017
Musil, A., Pejchal, J. & kol.: Stavební ročenka 1988, SNTL, Praha 1987
Sebok, T., Musil, A.: Study of rheological properties of consistent binding pastes, Cem. Concr. Res., USA 1986
Vynález č. 294888, Musil, A., van der Veen, A.: Způsob obnovení statiky panelových domů. UPV, Praha 2005
Vynález č. 307621, Musil, A.: Dvousložkový organický tmel pro stavebnictví. UPV, Praha 2019
Musil, A., Mitáček, P.: Přepěťované spoje. Materiály pro stavbu, ročník XXVIII, č. 4, s. 48-50, 2022
Musil, A., Mitáček, P.: Spoje na tupo. Materiály pro stavbu, ročník XXIX, č. 4, s. 57-59, 2023
Normy
- ČSN EN ISO 11600 (72 2331): 2004 Stavební konstrukce – Těsnící hmoty — Klasifikace a požadavky pro tmely
- ČSN EN ISO 7390 (72 2334): 2004 Stavební konstrukce – Těsnící hmoty – Stanovení stékavosti tmelů
- ČSN EN ISO 7389 (72 2333): 2004 Stavební konstrukce – Těsnící hmoty – Stanovení elastického zotavení tmelů
- ČSN EN ISO 8339 (72 2335): 2006 Stavební konstrukce – Těsnící hmoty – Tmely – Stanovení tahových vlastností (protažení při přetržení)
- ČSN EN ISO 10563 (72 2341): 2023 Tmely pro budovy a inženýrské stavby – Stanovení změn hmotnosti a objemu
- ČSN 72 2348: 1984 Zkoušení těsnících tmelů pro stavební účely. Stanovení tvrdosti elastických tmelů metodou podle Shore A











