Návrh, výpočet a posouzení stěn a detailů betonových konstrukcí

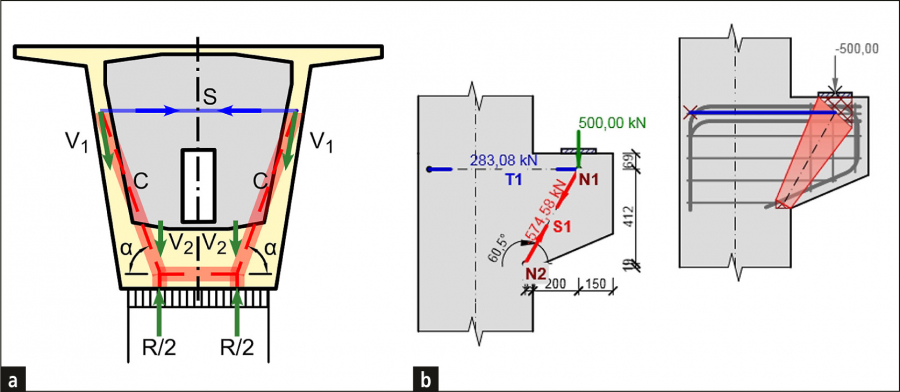
Každá betonová konstrukce obsahuje části s nějakou formou diskontinuity – krátkou konzolu, otvor, kotvení apod. V současné době se pro posouzení oblastí nespojitosti používají jednoúčelové specializované programy nebo excelovské tabulkové procesory založené na metodě příhradové analogie (obr. 1), nebo naopak mohou být výjimečně využity vědecky orientované programy bez vazby na národní normy a předpisy a bez možnosti návrhu a optimalizace výztuže. Tato praxe vede k přílišnému zjednodušování nebo naopak k pokusu zbytečně detailně simulovat realitu. Nová metoda a softwarový nástroj umožňují inženýrům efektivně, bezpečně a hospodárně navrhnout vhodné dimenze betonového prvku, umístění a množství výztuže, a to na základě platných norem.

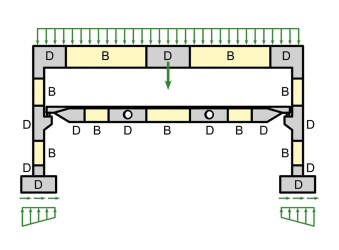
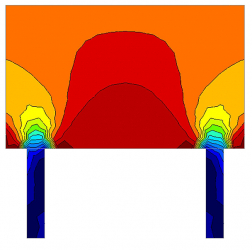
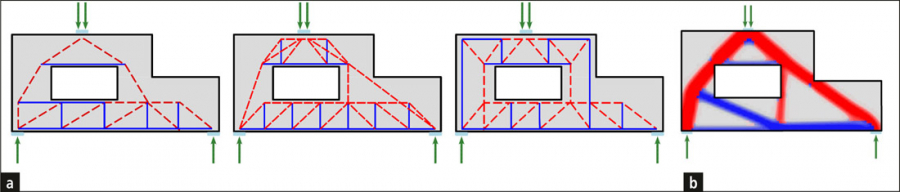
Návrh a posouzení betonových prvků běžně provádíme na úrovni řezu (prvky 1D) nebo bodu (prvky 2D). Tento postup je popsán ve všech normách pro dimenzování a je používán v každodenní praxi statika. Ne vždy se však ví či respektuje, že je možný pouze v oblastech, kde platí Bernoulliho-Navierova hypotéza o rovinnosti průřezu (tzv. B oblast). Místa, kde tato hypotéza neplatí, nazýváme oblasti diskontinuit neboli poruchové oblasti (D oblasti). Příklady B a D oblastí jsou u 1D prvků uvedeny na obr. 2. Jde o oblasti uložení, okolí osamělých břemen, místa změn průřezů, otvorů apod. Oblasti diskontinuit se vyskytují rovněž na stěnových prvcích monolitických a prefabrikovaných objektů. V současné praxi používané lineárně pružné deskostěnové modely tuto skutečnost sice výpočtem odhalí, viz obr. 3, ale nejsou schopny postihnout snížení tuhosti a přerozdělení napětí vlivem trhlin, tahové zpevnění, změkčení betonu v tlaku apod. Výsledkem řešení je pak barevný obrázek nereálných vnitřních sil a napětí s nedimenzovatelnými špičkami, přecenění tuhosti konstrukce, vznik a šíření trhlin a nadměrné průhyby. 

Příkladem může být obvodový plášť s otvory pro okna. Vysoké koncentrace v rozích v nadpraží ukáže i lineární výpočet. Poskytované výsledky jsou však nepřehledné a obtížná orientace v tom, jak vyztužit, vede ke vzniku trhlin v parapetech. Problémy vznikají dále např. v přechodech sloupového nosného systému na stěnový, viz obr. 3. Velký tlak ve sloupech v kombinaci s nedostatečným příčným vyztužením stěny způsobuje příčné rozestupování stěny, sloupy ji „propichují“ a vznikají téměř svislé trhliny.

Metody pro výpočet stěn a oblastí diskontinuit
Jak už jsme zmínili, části s nějakou formou diskontinuity obsahuje každá betonová konstrukce, a přesto doposud neexistuje žádné uživatelsky přívětivé, jasné a jednoznačné řešení pro kompletní návrh a posouzení betonových detailů, stěn a diafragmat.

Zájem statiků o spolehlivý a rychlý nástroj pro řešení oblastí diskontinuit vedl k rozhodnutí vyvinout nový výpočetní softwarový nástroj pro návrh a posouzení detailů a stěn železobetonových konstrukcí, který je dostupný pod názvem IDEA StatiCa Detail [1]. Tento program spojuje výhody a odstraňuje všechny výše uvedené nedostatky metod popsaných výše.

První výhodou metody, která se významně uplatňuje zejména u atypických detailů a stěnových konstrukcí, je možnost návrhu polohy a směrů výztuže metodou topologické optimalizace, viz [2], případně lineární analýzou, viz obr. 4. Zejména návrh příhradového modelu topologickou optimalizací identifikuje optimální místa uložení a směry výztuže, což může statikovi významně napomoci při rozhodování, jak danou konstrukci vyztužit. To neumožňuje žádná z doposud používaných metod. 

Metoda je založena na počítačové implementaci modelu tlakových polí. Uvažují se podobné zjednodušené předpoklady jako pro ruční výpočty, přitom však vylepšení modelu umožňuje řešení mezních stavů použitelnosti včetně deformací a je založeno na jasných materiálových vlastnostech. Model tlakových polí lze považovat za zobecněnou metodu příhradové analogie, ve které jsou však uvažovány skutečné oblasti namáhané napětím namísto výslednic sil. Ověření metody bylo provedeno vůči případům nezávislým na normách, jakož i porovnáním s výpočty podle existujících norem s materiálovými zákony definovanými těmito normami.

Návrh výztuže metodou topologické optimalizace
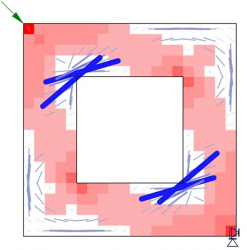
Nevýhodou dosavadních, výše popsaných metod je nejednoznačnost při stanovení polohy a směrů výztuže. V případě atypických detailů betonových konstrukcí se i zkušenému statikovi stává, že některá místa při návrhu výztuže podcení. Z tohoto hlediska je výhodnější použití metody příhradové analogie, která je jednoduchá, a proto je možné ověřit opakovanými výpočty různé příhradové modely. Existuje však nekonečné množství možných příhradových modelů a jen jeden z nich je optimální. Přitom neexistuje zaručený způsob, jak optimální model identifikovat (obr. 7). 

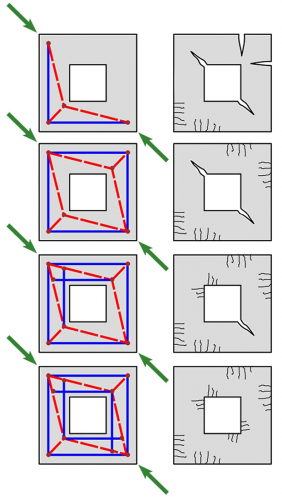
Jednou z možností, jak tento problém řešit, je návrh polohy a směrů výztuže metodou topologické optimalizace, viz [2]. Výpočtem lze identifikovat optimální místa uložení a směry výztuže, což může statikovi významně napomoci při rozhodování, jak danou konstrukci vyztužit. To neumožňuje žádná z doposud používaných metod.

Výpočtem se při topologické optimalizaci generuje automaticky geometrie náhradní příhradoviny použitím pouze určitého procenta původního objemu konstrukce a podle vhodných kritérií je uspořádána způsobem nejúčinnějším pro dané zatížení. To samozřejmě vede k nosné struktuře s řadou prázdných prostorů, kde není žádný materiál, což je praktické pouze při výrobě 3D tiskem. V případě železobetonových konstrukcí může tato geometrie být použita jako poměrně přesné vodítko pro identifikaci oblastí namáhaných jen tahem nebo jen tlakem. Tento proces se vlastně neliší od metody příhradové analogie, nicméně příhradovina se určí automaticky s mnohem menší potřebou manuální lidské práce a bez nutnosti opakovaných pokusů a omylů.

Princip výpočtu spočívá v maximalizaci celkové tuhosti hledané struktury pro danou množinu zatížení. To je ekvivalentní minimalizaci deformační energie, která se rovná práci prováděné vnějším zatížením. Optimalizovaná struktura se hledá iteračním algoritmem, přičemž se jako počáteční odhad geometrie struktury bere plná betonová konstrukce s homogenní hustotou materiálu a v jednotlivých krocích iterace se mění hustoty každého konečného prvku způsobem, který vede ke snížení celkové deformační energie.

Ve výpočtovém modelu je tuhost prvku úměrná jeho hustotě. Prvek se 100% hustotou má svou úplnou původní tuhost, zatímco prvek s 0% hustotou má nulovou tuhost. Výsledkem jsou po dosažení optima pouze prvky s hustotou 100 % nebo 0 %, které lze interpretovat jako místa, kde je materiál přítomen nebo není přítomen.

Přestože výsledky získané metodou topologické optimalizace stále vyžadují určitou míru reflexe a interpretace inženýra, věříme, že metoda představuje rychlý a snadno použitelný nástroj, který může výrazně usnadnit a urychlit návrh výztuže. To může vést k úspoře nejen v čase inženýra stráveném při návrhu, ale také v množství výztuže, které je třeba nezbytně použít.

Posouzení oblastí diskontinuit založené na platných normách
Jednou z metod pro statické řešení je nelineární analýza, která za předpokladu věrohodných vstupních údajů a modelu představuje nejvýstižnější způsob určení odezvy konstrukce. EN 1992-1-1 [3] povoluje použití nelineární analýzy pro prokázání odolnosti konstrukce ve všech mezních stavech únosnosti i použitelnosti, čehož využívá i nová metoda IDEA StatiCa. Častou otázkou však je, zda se mají pro nelineární analýzu použít pracovní diagramy vyjadřující co nejblíže skutečné (průměrné) vlastnosti materiálů, nebo pracovní diagramy pro navrhování průřezů. 

Použití průměrných vlastností pro fyzikálně-nelineární analýzu účinků návrhového zatížení vystihuje nejlépe realitu. Následné posouzení kritických oblastí s návrhovými hodnotami materiálových charakteristik ale vede většinou ke zvýšení množství výztuže ve druhém kroku řešení, a tedy k neekonomickému návrhu. Postup je navíc zdlouhavý, vede k opravám množství výztuže a dimenzí průřezů. Alternativně lze použít pravděpodobnostní přístup, ten je však s ohledem na náročnost a zdlouhavost doposud v praxi nerealizovatelný. 

Vhodným řešením se jeví metoda globálního součinitele odolnosti (global resistance factor method). Při určení návrhové odolnosti konstrukce je v tomto případě třeba vyrovnat se s faktem, že dílčí součinitele materiálu pro beton γ_c a výztuž γ_s se liší. Při použití skutečných (průměrných) vlastností materiálů by nebyla zajištěna stejná úroveň spolehlivosti při porušení betonu a při porušení výztuže. Proto je návrhová odolnost konstrukce získána pomocí skutečných (průměrných) vlastností výztuže a referenční hodnoty pevnosti betonu v tlaku. Návrhová hodnota účinků zatížení musí být potom menší nebo rovna podílu návrhové odolnosti konstrukce a ekvivalentního součinitele dílčí spolehlivosti materiálů (obvykle se uvádí γ_O’ = 1,27). V praxi se pak provádí výpočet tak, že se návrhová hodnota účinků zatížení proporcionálně zvyšuje až do okamžiku, kdy je dosaženo návrhové odolnosti konstrukce. Proporcionální násobek zatížení musí dosáhnout hodnoty alespoň γ_O’ = 1,27. Tímto způsobem lze prokázat mezní stavy únosnosti i použitelnosti pomocí jednoho nelineárního výpočetního modelu, přičemž metoda odpovídá požadavkům normy. Pro běžné použití v praxi se však i tato metoda jeví jako komplikovaná a nesrozumitelná.

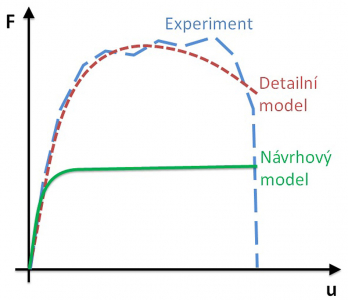
Z výše uvedených důvodů bylo proto pro posouzení mezního stavu únosnosti použito jednoduché a praktické řešení, tzv. návrhový model, což plně odpovídá v normě standardně používané metodě dílčích součinitelů odolnosti, viz obr. 8. To umožní přímé použití návrhových pracovních diagramů a posouzení na základě prvního kroku řešení. To sice může vést k určení nereálné odezvy konstrukce, protože pevnost betonu je součiniteli redukována mnohem víc než výztuž, metoda však dává konzervativní výsledky (na straně bezpečné). Vhodnou uživatelskou kombinací součinitelů zatížení a dílčích součinitelů materiálu je navíc možné v programu modelovat metodu globálního součinitele odolnosti.

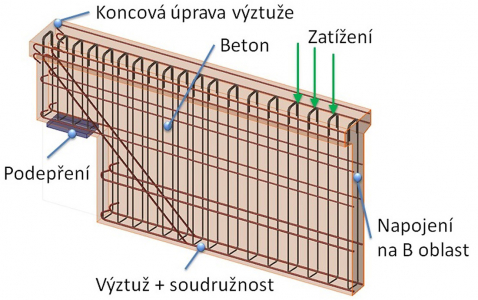
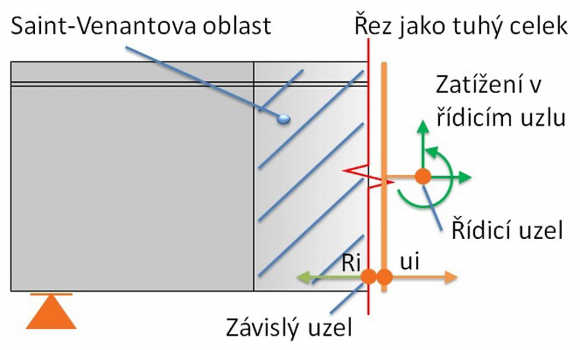
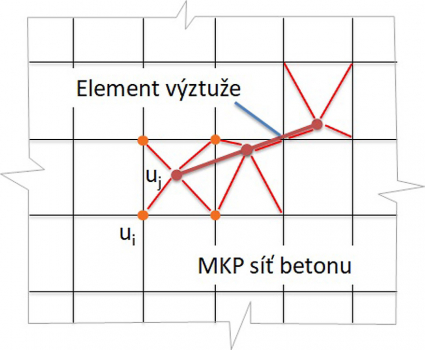
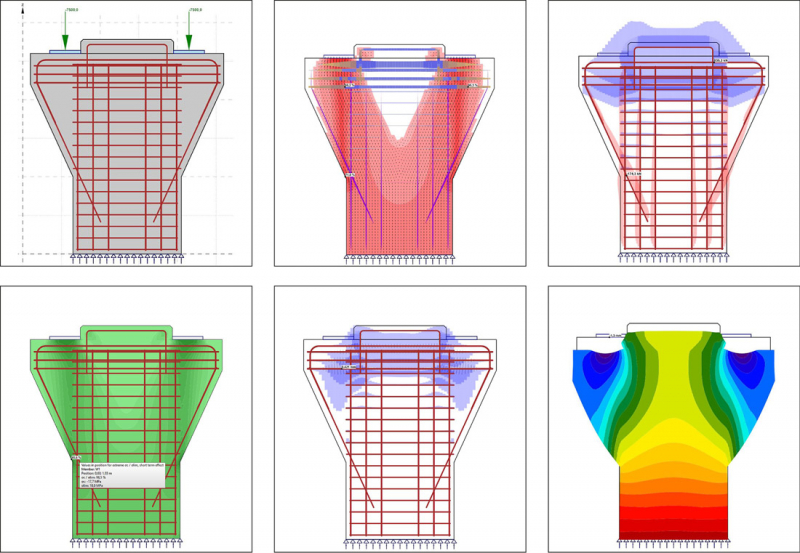
Nová metoda pro posouzení železobetonových stěn a detailů je tedy založena na nelineární analýze metodou konečných prvků. Výpočtový model je omezen na rovinnou napjatost, a to jak v případě analýzy stěn, tak i detailů 1D prvků (nosníků a sloupů), viz obr. 9. Betonové části konstrukce jsou modelovány isoparametrickými 2D stěnovými prvky (CQUAD4, případně CTRIA3). Výztužné pruty jsou modelovány včetně efektu tahového zpevnění (správněji ztužení) 1D pruty (CROD elements). Velmi důležitými částmi modelu jsou prvky, které zajišťují pevné vazby mezi parametry deformace v propojených bodech sítě. Každá vazba vyjadřuje jeden nebo více závislých stupňů volnosti jako lineární funkci nezávislých stupňů volnosti. Jsou implementovány tři typy vazeb (i) tuhá RBE2, (ii) interpolační prvek RBE3 a (iii) MPC vazba mezi skupinou uzlů. Prvek RBE3 lze také použít pro roznos zatížení do modelu. MPC se používá pro mapování deformace z betonové sítě na výztužnou síť, viz obr. 11. Všechny prvky jsou v modelu implementovány interně (neuživatelsky), počítačový program generuje model automaticky.

Podepření musí být v případě řešení stěn nebo celých 1D prvků staticky určité nebo neurčité, v případě řešení detailů (částí) 1D prvků může být i staticky přeurčité. V tom případě musí uživatel definovat řez, který simuluje napojení na B oblast, viz obr. 9 a 10. Mezi tímto řezem a zájmovou (řešenou) oblastí musí uživatel definovat dostatečně velkou Saint-Venantovu oblast, která se následně neposuzuje. Zatížení vnitřními silami se aplikuje v řídicím uzlu, na němž jsou závislé uzly stěny. Typy podpěr a vnějšího zatížení jsou znázorněny na obr. 12. Na konstrukci lze aplikovat rovněž rovnoměrné a plošné zatížení. Liniovou podpěru lze definovat jako nelineární (jen tlak).

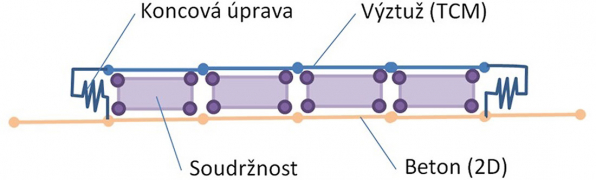
Osobitou vlastností nové metody je speciálně vyvinutý model soudržnosti a kotvení, viz obr. 13. Pro zajištění interakce výztužných prutů a betonových membránových (stěnových) prvků byl vyvinut speciální prvek soudržnosti. Napětí na prvku soudržnosti se řídí bilineární závislostí na pokluzu mezi výztužnou vložkou a betonem. Kotvení je modelováno přídavnou tuhostí (pružinou) na konci vložky. Tuhost pružiny se liší podle typu koncové úpravy. Kotevní síla se vypočítá na základě tuhosti pružiny s limitní hodnotou danou mezní pevností betonu v soudržnosti.

Pro řešení nelineární soustavy rovnic se v ak-tuální verzi programu používá Newton-Raphsonova metoda, která se z hlediska dohledání mezní hodnoty zatížení jeví pro většinu praktických případů dostatečná. 

Z hlediska fyzikálního je metoda založena na modelu tlakových polí s táhly, přičemž se předpokládají fiktivní rotující trhliny bez napětí v betonu v tahu (působení betonu v tahu je modelováno tahovým zpevněním táhla), nulový pokluz, průměrná poměrná přetvoření a maximální tahová napětí výztuže v trhlině, kde je rovněž maximální tlakové napětí v betonu. Směry hlavních napětí a hlavních přetvoření se shodují, čímž je ve stavu po vzniku trhlin odděleno chování v obou hlavních směrech s výjimkou efektu tlakového změkčení (redukce pevnosti betonu v tlaku v důsledku příčného přetvoření v tahu. Tlakové změkčení se počítá automaticky v závislosti na dvouosé napjatosti v daném bodě. 

Konstitutivní vztahy pro beton vycházejí ze standardního parabolicko-rektangulárního pracovního diagramu v jednoosém namáhání, který je známý z [3] a který se odvozuje pouze z třídy betonu, resp. z jeho pevnosti v tlaku. Chování betonářské oceli se ve výchozím nastavení popisuje idealizovaným bilineárním pracovním diagramem rovněž známým z norem pro navrhování. Pro zohlednění vlivu tahového zpevnění se u výztužných vložek zabudovaných do betonu zavádí modifikace pracovního diagramu. Model tahového zpevnění rozlišuje případy stabilizovaného a nestabilizovaného rozdělení trhlin. V případě plně rozvinutých stabilizovaných trhlin se pro vyjádření tahového zpevnění používá tzv. Tension Chord Model (TCM). S ohledem na to, že v TCM závisí tahové zpevnění na stupni vyztužení a na jeho přiřazení ke každé výztužné vložce či vrstvě, je určení příslušné účinné tažené (spolupůsobící) plochy betonu zásadní. Z toho důvodu byla implementována automatická prostorová (3D) identifikace odpovídající účinné tažené plochy betonu pro libovolnou konfiguraci výztuže. 

Implementace modelu pro případy nestabilizovaného rozdělení trhlin se v programu předpokládá ve druhé polovině roku 2018. Z toho důvodu je možné aktuálně posuzovat šířku trhlin jen v oblastech se stupněm vyztužení větším než 0,6 %. Podrobný popis fyzikálního modelu lze nalézt v [4]. 

Závěr
Podobně jako metoda příhradové analogie, je zadání úlohy, návrh výztuže, výpočet a posouzení velmi rychlé a lze jej provést, na rozdíl od obecných nelineárních programů, v řádu 10 až 20 minut. Předpoklady řešení jsou nad úrovní normou předpokládaných modelů, veškeré výsledky jsou však interpretovány plně z hlediska normových ustanovení [3], takže pro porozumění poskytovaným výsledkům není třeba žádné speciální zkušenosti či znalosti. Metody použité pro výpočet a posouzení jsou obecné jak z hlediska topologie řešených oblastí, tak z hlediska poskytovaných výsledků. Výsledky jsou srozumitelné a maximálně výstižné, mohou sloužit nejen k posouzení MSÚ, ale i MSP včetně šířky trhlin, průhybů a omezení napětí, viz obr. 14. Model byl verifikován a validován včetně všech parametrů vstupujících do výpočtu prestižním Ústavem stavebního inženýrství ETH Zürich [4].
JAROSLAV NAVRÁTIL, PETR ŠEVČÍK, JAROMÍR KABELÁČ

Poděkování
Tento projekt získal finanční podporu z programu Eurostars-2, projekt ID 10 571 a MŠMT ČR Eurostars-2-7D16010 se spolufinancováním z výzkumného a inovačního programu EU Horizont 2020. Související software IDEA StatiCa Detail byl vyvinut společností IDEA StatiCa ve spolupráci s Ústavem stavebního inženýrství ETH Zürich. Kromě autorů článku se na projektu rovněž podíleli vývojáři Petr Foltyn, Libor Michalčík, Michal Číhal, Rostislav Krč, Filip Svoboda, Filip Adler, Michael Konečný a kolektiv výzkumných pracovníků IBK ETH Zürich pod vedením prof. Kaufmanna.

Literatura:
1) IDEA StatiCa, User guide, IDEA StatiCa, s. r. o., www.ideastatica.com.
2) KONEČNÝ, M., KABELÁČ, J., NAVRÁTIL, J. Use of topology optimization in concrete reinforcement design, In: Sborník ke konferenci 24. Betonářské dny 2017.
3) EN 1992-1-1 Eurocode 2, Design of Concrete Structures – Part 1: General rules and rules for buildings, European Committee for Standardization, December 2004–2016.
4) MATA-FALCÓN, J., TRAN, D., T., KAUFMANN, W., NAVRÁTIL, J. Computer-aided stress field analysis of discontinuity concrete regions, In: Proceedings of EURO-C 2018 Computational Modelling of Concrete and Concrete Structures, Austria, 2018, in print.
5) NAVRÁTIL, J., ŠEVČÍK, P., MICHALČÍK, L., FOLTYN, P., KABELÁČ, J. Řešení stěn a detailů betonových konstrukcí, In: Sborník ke konferenci 24. Betonářské dny 2017. 

Doc. Ing. Jaroslav Navrátil, CSc., (*1962)
absolvoval Fakultu stavební Vysokého učení technického v Brně. Pracuje jako hlavní řešitel a garant projektu DR-Design Eurostars-2 pro vývoj nového inovativního softwarového nástroje pro automatizovaný a optimalizovaný návrh a posouzení oblastí diskontinuit betonových prvků a konstrukcí. Specializuje se na výpočetní metody pro návrh, statickou analýzu a posouzení stavebních konstrukcí. Publikoval řadu odborných článků, výzkumných zpráv, expertiz a učebnici Předpjaté betonové konstrukce.

Ing. Petr Ševčík (*1969)
absolvoval Fakultu stavební Vysokého učení technického v Brně. Pracuje jako vedoucí vývojový pracovník pro oblast betonových prvků a konstrukcí ve firmě IDEA StatiCa, s. r. o. Specializuje se na vývoj software pro dimenzování, pro vyztužování betonových prvků a na návrh uživatelského prostředí.

Ing. Jaromír Kabeláč, Ph.D., (*1975)
absolvoval Aplikovanou mechaniku na VUT v Brně. Pracuje jako vedoucí vývojový pracovník konečně prvkového systému pro Idea StatiCa, s. r. o. Specializuje se na vývoj metod pro numerické simulace.

Máte-li požadavek na doplnění či rozšířejní tohoto tématu nebo k němu chcete autorsky sami přispět dalšími informacemi, piště do redakce na mas@bmone.cz.