Použití infračervené termografie jako metody bezkontakní diagnostiky příčin vad a poruch ETICS je poměrně známé a dobře popsané viz např. [1] a [2]. Výhody této metody jsou zřejmé: při použití infračervené kamery odborníkem lze získat přesné vyjádření teplotního pole a velice snadno zjistit např. to, kde jsou v zateplované konstrukci tepelné mosty, kde dochází ke kondenzaci vodní páry apod. Získané snímky, tzv. termogramy, jsou i pro laika srozumitelné a lze na nich názorně ukázat na problém nacházející se uvnitř konstrukce.
Pomocí infračervené termografie lze měřit jak detaily stavby, tak stavbu jako celek. Přitom ceny za infračervené kamery klesají a stávají se poměrně dostupnými. Bohužel, použití infračervené termografie není možné celoročně. Také celou řadu špatně navržených detailů již ve fázi projektové přípravy nelze pomocí této metody odhalit, popř. výsledky mohou být zavádějící a ukazovat např. na nepodařenou realizaci. Je tedy dobré pro posuzování vad a poruch detailů ETICS zavést ještě další podpůrnou metodu, která může odhalit chyby v návrhu ETICS, popř. pomocí které by bylo možné provést analýzu detailu i v tom období v roce, kdy není zajištěn teplotní gradient mezi interiérem a exteriérem min. 20 K.
Cílem článku je ukázat, že analýza detailu ETICS pomocí 3D modelování teplotního pole s použitím metody konečných prvků (MKP) může dávat relevantní a poměrně přesné výsledky, a že ji tedy můžeme použít i v soudně inženýrské praxi. Aby bylo možno s důvěrou tuto metodu použít, bylo provedeno i porovnání výsledků analýz MKP s měřením pomocí infračervené termografie.

3D teplotní pole a metoda konečných prvků (MKP)
3D teplotní pole řešíme tam, kde řešení rovinné, tedy 2D, nestačí. Bude se nejčastěji jednat o styk tří na sebe navazujících konstrukcí, typicky např. styk dvou obvodových stěn a stropní konstrukce nebo podlahy. Tento detail ve své složitosti již nelze komplexně řešit a popsat pomocí metod 2D šíření tepla, tak jak se tomu běžně děje u posuzování např. detailu základové konstrukce navazující na obvodovou stěnu.
Řešení teplotního pole může být provedeno jednak metodou sítí, kdy se vychází z předpokladu řešení diferenciální rovnice toku tepla s konečnými rozdíly, které se zjednoduší na lineární rovnici [3], nebo se může řešení provést pomocí metody konečných prvků (MKP). Základ této metody spočívá v uplatnění tzv. Galerkinovy metody, se kterou ve 20. letech 20. století přišli ruští vědci Ivan Bubnov a Boris Grigorevič Galerkin. Podstatou metody je speciální postup při řešení parciálních diferenciálních rovnic spočívající v nahrazení původní rovnice její integrální formou. Oba ruští vědci navázali na práci německého matematika Walthera Ritze, a někdy tedy metoda nahrazení bývá též označována jako Ritz-Galerkinova. Vážnější uplatnění MKP nastalo samozřejmě až s rozvojem výpočetní techniky a dnes je MKP používána k simulaci nejrůznějších fyzikálních polí a nemusí to nutně být pouze teplotní pole. Běžně je MKP používána k simulaci napětí ve stavebních konstrukcích, elektrostatického pole v elektrotechnice apod.
Třírozměrné stacionární teplotní pole lze popsat parciální diferenciální rovnicí:
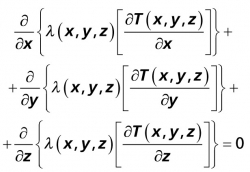 (1)
(1)
Pro tuto rovnici platí okrajová podmínka:
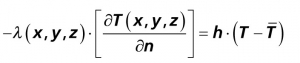 (2),
(2),
kde
x, y, z … jsou souřadnice bodu v rovině [m],
λ … součinitel tepelné vodivosti [W/m.K],
T … teplota v bodě [K],
h … součinitel přestupu tepla [W/m².K],
T … teplota v okolním prostředí [K],
δx, δy, δz … derivace podle x, y a z,
δn … derivace podle normály.
Rovnice (1) se řeší na souvislé oblasti Ω s hranicí Γ, na které musí být splněna okrajová podmínka (2), přičemž hranice Ω je pravoúhlá. Dále se předpokládá, že oblast Ω může být dále rozdělena na konečný počet oblastí, ve kterých je funkce λ(x, y, z) konstantní. Také funkce α(x, y, z) a T(x, y, z) jsou uvažovány jako konstantní po částech hranice Γ. Zde již přichází na řadu Galerkinova metoda, kdy s pomocí Greenovy věty převádíme rovnici (1) na tvar:
![]() (3),
(3),
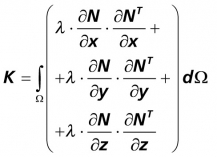 (4),
(4),
 (5),
(5),
kde
K … je matice vodivosti tělesa,
r … sloupcová matice uzlových hodnot teploty (neznámých),
q … vektor pravé strany (vektor zdrojů),
N … řádková matice bázových funkcí.
Řešení MKP s použitím k tomu určenému software v zásadě vychází z rovnice (1). Každý uzlový bod řešeného detailu má určitou pozici na souřadnicích x, y, z s definovanými okrajovými podmínkami a materiálovými charakteristikami. Jelikož počítač nemůže řešit spojité diferenciální rozdíly mezi jednotlivými uzlovými body, musí dojít k převodu na diskrétní konečný počet prvků oblasti, na kterých dojde k analýze.
Z výše uvedeného vyplývá, že pro úspěšné zvládnutí vytvoření 3D modelu, na kterém bude provedena simulace, je nutná poměrně pečlivá příprava sítě a oblastí s homogenním materiálem (např. ocelová kotva v zateplovacím systému, který je aplikován na obvodovou zděnou konstrukci). K tomuto problému přistupují výpočtové programy různě, některé umožňují import 3D modelu z jiného modelovacího nebo stavebního software, u jiných je nutné celý 3D model kompletně zadat pomocí os a oblastí bez možnosti importu vymodelovaného detailu.
Zatímco pro modelování 2D teplotního pole existuje celá řada systémů, některé jsou dokonce zdarma distribuovány jako open source, je situace na poli 3D systémů poněkud omezená. Některé softwary jsou určeny pro obecné modelování jakéhokoliv fyzikálního pole a je na uživateli, jestli to bude zrovna teplotní pole, např. ANSYS, jiné jsou určeny přímo pro modelování 3D teplotního pole – např. software doc. Svobody CUBE 3D.
Pro soudně inženýrskou praxi může být modelování 3D teplotních polí pro účely diagnostiky detailů vnějších zateplovacích systémů (ETICS) přínosné zejména v situacích, kdy nelze použít diagnostiku infračervené termografie. Jedná se zejména o tu část roku, kdy nelze zajistit teplotní rozdíl mezi interiérem a exteriérem alespoň 20 K.
Pro ověření reálnosti použití diagnostiky pomocí modelování 3D teplotního pole v praxi je nutné srovnat výsledky pořízené infračervenou kamerou s vymodelovaným detailem a zjistit, do jaké míry odpovídá výpočet MKP realitě.
Srovnávací metoda
K ověření možnosti použít výsledky 3D modelování teplotního pole pomocí MKP jsem přistoupil k analýze infračerveného snímku detailu pořízeného termokamerou FLIR e60 a výsledku modelování 3D teplotního pole na témže detailu v software CUBE 3D. Pro skutečně průkazné srovnání a relevantní závěr jsem vymodeloval celkem 22 různých detailů různých částí panelového domu, postaveného v konstrukční soustavě T0B-BU, a na těchto detailech provedl měření pomocí infračervené kamery. Některé detaily byly vymodelovány jako konstrukce bez zateplení a po zateplení, byly tedy analyzovány dva stavy. Naprosto stejně bylo provedeno měření pomocí infračervené termografie, a to na téže stavbě. Měření bylo provedeno v rámci dvou zimních sezón, nejdříve pro případ, kdy ještě nebylo provedeno zateplení a další zimu, a kdy již bylo provedeno zateplení.
Měření a porovnávání detailů právě na konstrukční soustavě panelového domu není náhodné. V současnosti se jedná o nejčastěji zateplované typy staveb. Pro naše účely jsem vybral detail lodžie. Lodžie probíhá přes celý rozpon konstrukční soustavy, tj. 6,0 m, stěny lodžie jsou v našem případě široké 200 mm a skládají se z železobetonových panelů a vložené tepelné izolace z pěnového polystyrenu (EPS) tl. 40 mm. Na stěnu lodžie navazuje štítový panel tl. 290 mm s EPS tl. 80 mm a dále průčelní panel s izolací EPS také o tl. 80 mm. Na tomto detailu bylo provedeno měření infračervenou kamerou nejdříve pro nezateplenou lodžii a pro zateplenou lodžii (v další sezóně). Pro ověření správnosti infračerveného měření bylo provedeno ještě třetí měření na jiném panelovém domě ve stejné konstrukční soustavě, a to stejného detailu vždy v tentýž den a za téměř stejných podmínek. Teplota vzduchu byla naměřena na –1,0 °C, teplota interiéru byla zjištěna od nájemníků a činila 21 °C. Tyto údaje byly dále použity pro zadání okrajových podmínek při modelování teplotního pole. Cílem je zjištění, jestli teplotní pole detekované infračervenou kameru odpovídá modelovanému teplotnímu poli.
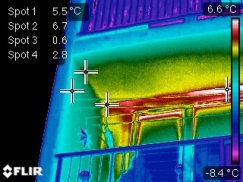


Na obr. 1 je panelový dům postavený v konstrukční soustavě T08-BU, na kterém bylo provedeno měření detailu lodžie. Jednalo se o pravou lodžii umístěnou v 2. patře. Detail byl vymodelovaný v software CUBE 3D a na tomto detailu byly nastaveny okrajové podmínky odpovídající naměřeným hodnotám teplot interiéru a exteriéru. Materiálové parametry jednotlivých vrstev sendviče panelů lodžie byly zadány v souladu s ČSN 73 0540. Na obr. 2 je vyobrazeno měření tohoto detailu pomocí infračervené kamery ve stavu před zateplením a na obr. 3 po zateplení pěnovým polystyrenem tl. 140 mm.
Dále byl nasnímán detail styku štítového panelu a lodžiového panelu před zateplením, jak ukazuje obr. 4. I tento detail (znázorněný na obr. 4) byl vymodelován a analyzován pomocí MKP. Na obr. 5 a 6 jsou uvedeny výstupy z programu CUBE 3D, ve kterém byly uvedené detaily modelovány.
V prvé řadě si je nutné uvědomit, že barevná paleta modelovaného detailu odpovídá zadání okrajových podmínek, tj. jsou zde teplotní pole s hodnotami od 21 °C do –1,0 °C, zatímco u detailu nasnímaného infračervenou kamerou je barevná škála podrobnější, jelikož rozsah snímaných teplot je podstatně menší. Zabarvení detailu v měřených místech (do modré barvy) odpovídají teplotám 2,8–4,7 °C. Pokud bychom detail modelovali mnohem podrobněji s použitím hustší sítě uzlových bodů, přiblížili bychom se velice blízko výsledkům infračervené kamery. Při patřičném zvětšení detailu zasahuje oblast s teplotami od 0,9 do 2,8 °C k třetině vyložení balkonu lodžie. Pokud srovnáme infračervený snímek s modelem, zjistíme, že dochází k rozdílu mezi měřenými a zjištěnými teplotními poli zhruba 1,2 °C. To může být dáno zejména skutečností, že při modelování lze velice těžko do analýzy zapracovat materiálové poškození tepelné izolace a tím pádem se jen velice těžko odhaduje hodnota součinitele tepelné vodivosti λ. Také nemusí být naprosto přesně zadány materiálové charakteristiky vyztuženého betonu panelů. Jemné doladění těchto parametrů bude vyžadovat další výzkum, který ukáže, jak se např. vyvíjí hodnota součinitele λ v závislosti na stáří materiálů právě ve sledovaných případech. Obdobné výsledky obdržíme při srovnání vymodelovaného detailu tentokrát zateplené lodžie (obr. 6) s detailem infračerveného snímku z obr. 3.

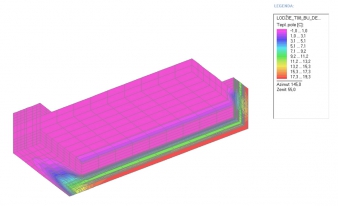
Zateplení jak průčelního panelu, tak i stěny lodžie výrazně snížilo teploty teploního pole, které se nyní pohybují podle odstínu v rozmezí od 0,0 do 1,5 °C. Výsledek tedy odpovídá snímku z infračervené kamery. U zatepleného detailu se ukazuje, že je výsledek mnohem méně ovlivněn odhadem materiálových charakteristik původních materiálů, což bude nejspíše způsobeno podstatně vyšším tepelným odporem R tepelného izolantu ETICS.
Závěr
Výsledky analýz modelování 3D teplotních polí pomocí MKP, které popisují zkoumaný detail v celé jeho komplexitě, poskytují jednoznačně relevantní výsledek, jehož přesnost je dána především tím, jak zvolíme hustou síť uzlových bodů, ve kterých dochází k analýze. V soudně inženýrské praxi se může jednat o přínosnou diagnostickou metodu, pomocí které je možné zkoumat příčiny např. kondenzace vodní páry uvnitř konstrukce a její vliv na vznik konkrétní vady či poruchy ETICS. Ověření přesnosti MKP a její možné využití bylo provedeno pomocí kontrolního snímkování detailů infračervenou termografií. Infračervené snímky potvrzují, že výsledky analýzy 3D modelování teplotního pole jsou poměrně přesné a využitelné v praxi. Ukazuje se však, že je nutné dále zkoumat vliv stáří na materiálové charakteristiky materiálů, ze kterých se daný detail skládá. Vliv stáří by se dal uvažovat jednoduchým koeficientem, kterým by se nepatrně měnila hodnota tepelné vodivosti λ. Tím by bylo možno dosáhnout přesnějších výsledků.
ALEŠ ZVĚŘINA
foto archiv autora
Recenzoval doc. Ing. Miloš Kalousek, Ph.D., VUT v Brně, FAST, Ústav pozemního stavitelství.
Literatura:
1) KALOUSEK, Miloš. Termovizní diagnostika betonových konstrukcí. Sanace betonových konstrukcí, roč. 17, č. 1, 2004, Praha. ISSN: 1211-3700.
2) ZVĚŘINA, Aleš, Miloš KALOUSEK. Bezkontaktní diagnostika vad a poruch vnějších kontaktních zateplovacích systémů pomocí infračervené termografie. Brno: VUT v Brně, ÚSI, 2010. ISBN 978-80-214-4276-4.
3) VAVERKA, Jiří. Stavební tepelná technika a energetika budov. Brno: VUTIUM. 2006. ISBN 80-214-2910-0.
4) ČUPROVÁ, Danuše, Miloš KALOUSEK. Modelování tepelných mostů. Ateliér otvorových výplní, izolací a vybavení staveb. 2005, roč. 9, č. 5, s. 14. ISSN-1212-4370.
5) ŠUBRT, Roman, Pavlína ZVÁNOVCOVÁ a Martin ŠKOPEK. Katalog tepelných mostů. České Budějovice: Energy Consulting, s. r. o., 2008. ISBN 978-80-254-2715-6.
Ing. Aleš Zvěřina (*1974)
je absolventem Technické fakulty České zemědělské univerzity. Celou profesní kariéru pracuje jako projektant pozemních staveb, je jednatelem a vedoucím projektantem společnosti Inveko.eu, s. r. o., a současně doktorandem v Ústavu soudního inženýrství VUT v Brně.










