Kompozitní dřevobetonové stropy se používají především při zesilování stávajících stropů s dřevěnými stropními nosníky. Provedením betonové desky, kterou spřáhneme s dřevěnými nosníky pomocí různých spřahovacích prostředků, výrazně zvýšíme tuhost i únosnost stropní konstrukce. Kompozitní dřevobetonové stropní konstrukce mají též lepší parametry kročejové a vzduchové neprůzvučnosti a požární odolnosti oproti tradičním dřevěným stropům.
Problematika navrhování kompozitních dřevobetonových nosníků je již zapracována do eurokódů, které byly zavedeny do soustavy ČSN v České republice jako ČSN EN. Kompozitní dřevobetonové konstrukce lze zjednodušeně řešit s využitím ČSN EN 1992-1-1, ČSN EN 1995-1-1 a ČSN EN 1995-2 následujícím způsobem.Návrh kompozitního dřevobetonového průřezu je popsán v článku 5.3 ČSN EN 1995-2 s tím, že šířka betonové desky, která spolupůsobí se dřevěným nosníkem bef,c, se určí podle článku 5.3.2.1 ČSN EN 1992-1-1.
Kompozitní dřevobetonový T-průřez se potom posoudí podle přílohy B ČSN EN 1995-1-1, která je věnována nosníkům složeného průřezu s mechanickými spojovacími prostředky, přičemž hodnoty modulu prokluzu pro spoj beton – dřevo jsou uvedeny v článku 7.1 této normy. Tento postup lze ale použít pouze v případě, že mezi dřevěným nosníkem a betonovou deskou není mezilehlá vrstva, např. bednění. Výpočet podle ČSN EN je konzervativní a hodnoty únosnosti a tuhosti spřažení pomocí spřahovacích prostředků kolíkového typu jsou přibližné. Na základě provedené analýzy únosnosti a tuhosti spřahovacích prostředků, viz dále, bylo zjištěno, že především tuhost určovaná podle ČSN EN 1995-1-1 je cca o 20 % nadhodnocována, neboť norma předpokládá, že spřahovací prostředek je v betonu dokonale vetknut a při zatížení nedochází k jeho zatlačení do betonu. Dalším důležitým poznatkem je, že jakost betonu má vliv na únosnost spřahovacích prostředků ve spojích dřevo – beton, ale nikoliv již na jejich tuhost.
Jestliže budeme předpokládat, že se spřahovací prostředek kolíkového typu ve spoji dřevo – beton s mezivrstvou deformuje podle obr. 2 vlevo, můžeme zapsat rovnici rovnováhy (1) k bodu A pro mezní stav únosnosti spřahovacího prostředku – viz obr. 2 vpravo.
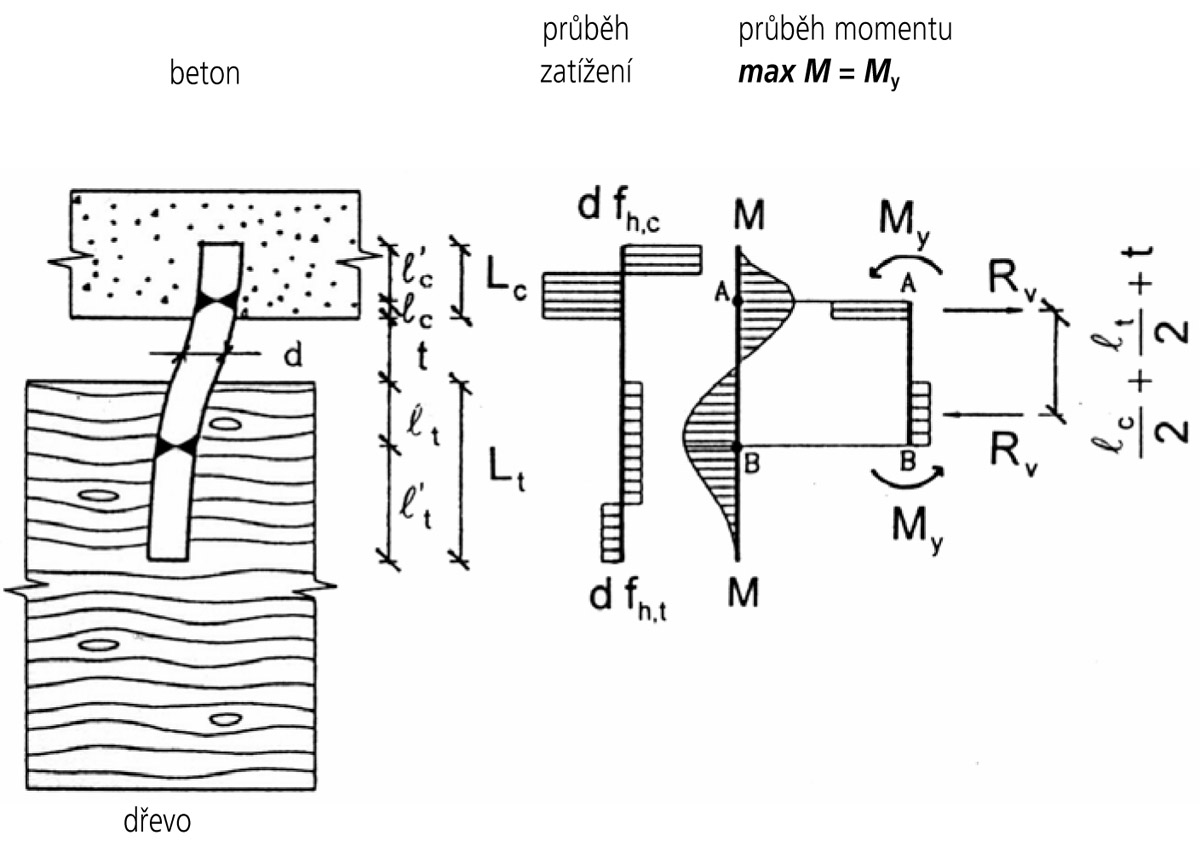
Za předpokladu, že
platí
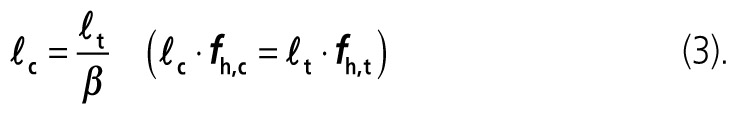
Únosnost spřahovacího prostředku podle Johansenovy teorie se potom rovná:
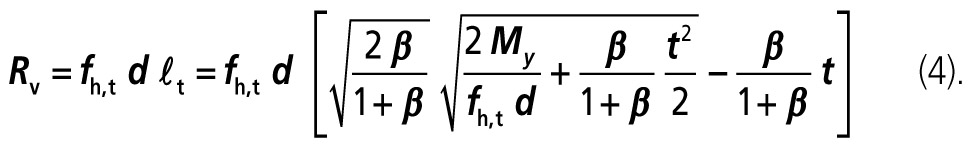
V případě spřažení bez mezivrstvy (t = 0) se vztah pro Rv zjednoduší na vztah:
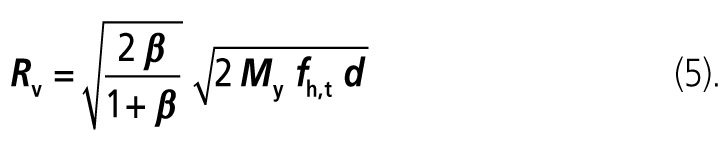
Uvedené vztahy platí pro spřahovací prostředek, u kterého se současně vytvoří dva plastické klouby. To nastane za předpokladu, že:
Při navrhování spřahovacích prostředků kolíkového typu se dvěma plastickými klouby je proto třeba dodržet délky jejich průniku do dřeva a betonu:
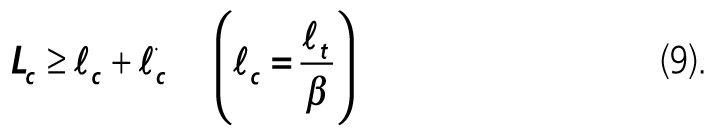
Vztahy (4) a (5) řeší únosnost spřahovacích prostředků pouze podle Johansenovy teorie. Při deformačním tvaru (viz obr. 2) však spřahovací prostředek bude též namáhán osovou silou, která vzniká od jeho ohybu a ukotvení do dřeva a betonu.
Tato osová síla bude k sobě přitlačovat betonovou desku a dřevěný nosník a zvyšovat tak únosnost spřahovacího prostředku. Na zvýšení únosnosti spřahovacího prostředku se též bude podílet složka osové síly ve skloněné části spřahovacího prostředku, působící rovnoběžně se spárou mezi dřevem a betonem.
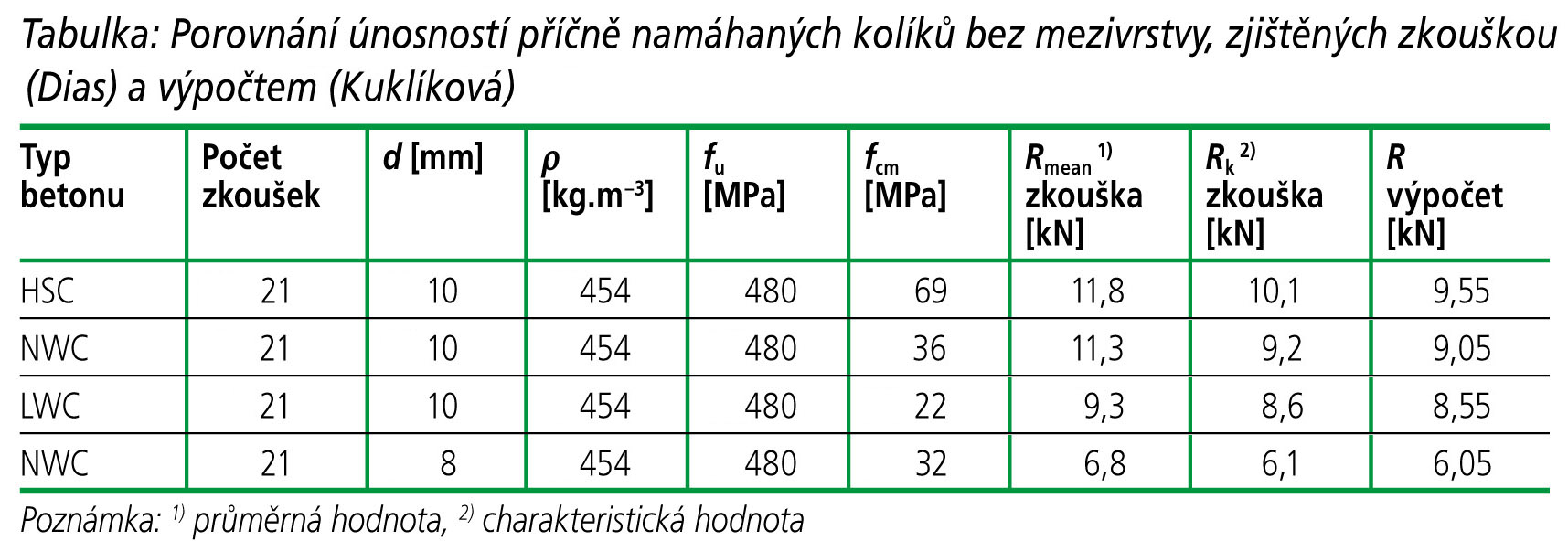
Kalibrací experimentů se ukazuje, že nárůst únosnosti spřahovacího prostředku namáhaného příčně nejlépe vystihuje (viz tabulka) tento vztah:
Podmínkou pro použití odvozených vztahů je znalost pevnosti betonu v otlačení fh,c. Při řešení tohoto problému byly využity výsledky výzkumu spřažených konstrukcí beton – beton (Hrdoušek, 1993).
Z rozboru poznatků prezentovaných ve výzkumné zprávě (Hrdoušek, 1993) vyplynulo, že hodnotu pevnosti betonu v otlačení fh,c je možné uvažovat jako čtyřnásobek průměrné hodnoty válcové pevnosti betonu v tlaku fcm. Tomuto odpovídá též deformační tvar hřebíku na obr. 1, neboť lt a lc (podle obr. 2) odpovídají předpokladům rovnic (2) a (3).
Spřažení pomocí kolíků
V případě, kdy bude jako spřahovací prostředek použit ocelový kolík, je možné použít následující vztahy (Whale, 1987) pro pevnost dřeva v otlačení fh,t a plastický moment únosnosti My. Únosnost kolíků na vytažení je tak malá, že se zanedbává.
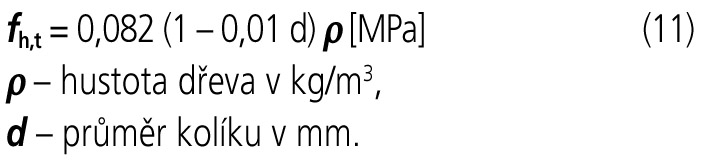
Poznámka:
Plastický moment únosnosti ocelového kruhového průřezu se určuje ze vztahu:
U ocelových spřahovacích prostředků za studena tvářených mez kluzu fy není tzv. vyznačena a rovná se přibližně 80 % meze pevnosti fu. U dřevěných konstrukcí se proto pro určení plastického momentu únosnosti kolíku často používá vztah
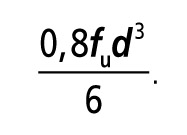
Protože podle tohoto vztahu vycházejí hodnoty plastického momentu únosnosti vyšší než podle ohybových zkoušek, je možné též používat konzervativnější vztah (12). Pomocí tohoto vztahu byly též určeny únosnosti kolíku uvedené v tomto článku.
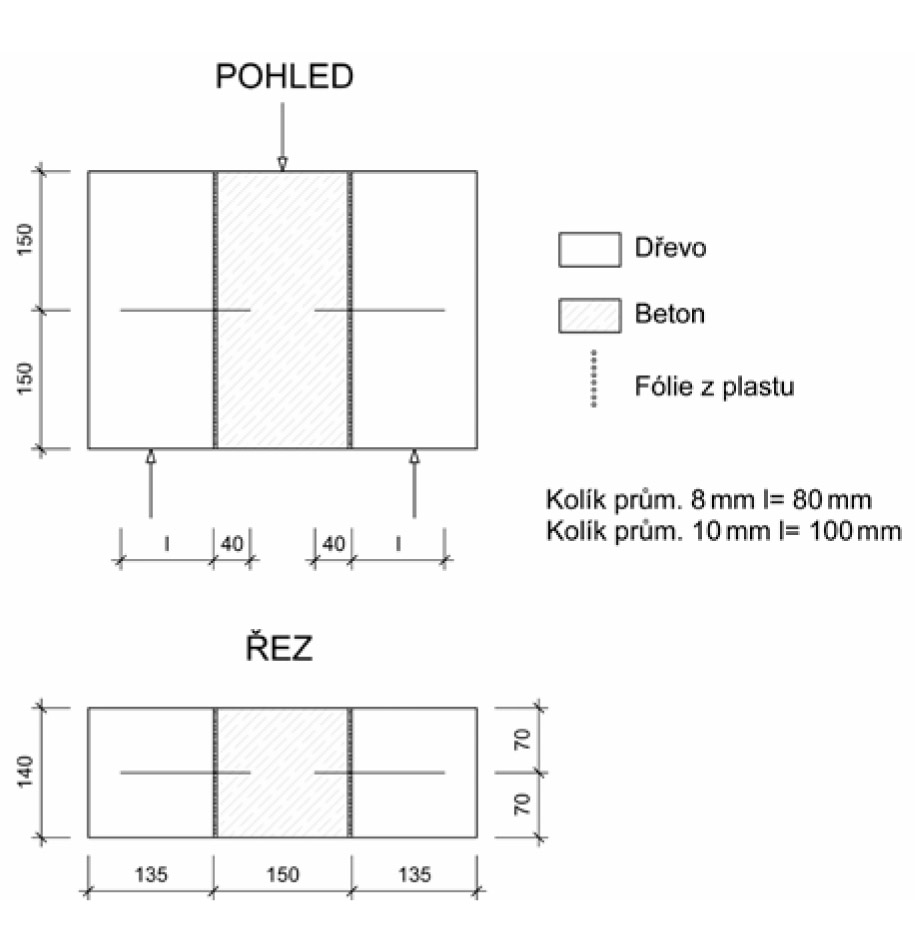
Pro ověření platnosti předchozích vztahů byly použity výsledky protlačovacích zkoušek, které byly provedeny na univerzitě v Coimbře (Dias, 2003) a ČVUT v Praze, Fakultě stavební (Kuklíková, 2004). Zkušební tělesa (viz obr. 3) byla provedena ze smrkového řeziva a betonu různých pevností (HSC – vysokopevnostní beton, NWC – obyčejný beton, LWC – lehký beton). Použity též byly kolíky dvou různých průměrů: 8 a 10 mm.
Porovnání únosností kolíků zjištěných zkouškou a výpočtem podle rovnic (2), (5), (10), (11) a (12) je provedeno v tabulce.
Závěr
Z hodnot uvedených v tabulce vyplývá, že únosnosti kolíků zjištěné podle analyticky odvozených výpočetních vztahů (Kuklíková, 2004) se velmi dobře shodují s charakteristickými hodnotami zjištěnými zkouškou. Výpočet též velmi dobře zohledňuje změnu jakosti betonu.
ANNA KUKLÍKOVÁ, PETR KUKLÍK
foto archiv autorů
Tento příspěvek byl zpracován za podpory VZ ČVUT v Praze MSM 6840770001 „Spolehlivost, optimalizace a trvanlivost stavebních materiálů a konstrukcí“.
Literatura:
1) Dias, A. – J. W. G. Kuilen – Cruz, H.: Mechanical properties of timber-concrete joints made with steel dowels, Coimbra University, 2003.
2) H rdoušek, V. – Krátký, J. – Křečan, J. – Kukaň, V. – Procházka, J. – Šmerk, P.: Spřažené konstrukce beton-beton, ČVUT Praha, 1993.
3) Johansen, K. W.: Theory of timber connections. International Association of Bridge and Structural Engineering. Publication No. 9:249-262. Bern, 1949.
4) Koželouh, B.: Zkoušky těles spřažených ze dřeva a betonu, ŠDVU Bratislava, 1975.
5) Kuklík, P.: Navrhování dřevěných konstrukcí, Technická knižnice autorizovaného inženýra a technika, ČKAIT, Praha, 1997.
6) Kuklíková, A.: Kompozitní dřevobetonové konstrukce, ČVUT v Praze, 2004.
7) Whale, L. R. J. – Smith, I. – Larsen, H. J.: Design of nailed and bolted joints, proposals for the revision of existing formulae in draft Eurocode 5 and CIB code, Paper 20-7-1, Proceedings CIB – W18 meeting, Dublin, Ireland 1987.
8) ČSN EN 26891: Dřevěné konstrukce. Spoje s mechanickými spojovacími prostředky. Všeobecné zásady pro zjišťování charakteristik únosnosti a přetvoření (732070), ČSNI, Praha, 1994.
9) ČSN EN 1992-1-1 Navrhování betonových konstrukcí. Část 1-1: Obecná pravidla a pravidla pro pozemní stavby, ČNI, Praha, 2006.
10) ČSN EN 1995-1-1 Navrhování dřevěných konstrukcí, Část 1-1: Obecná pravidla a pravidla pro pozemní stavby, ČNI, Praha, 2006.
11) ČSN EN 1995-2 Navrhování dřevěných konstrukcí Část 2: Mosty, ČNI, Praha, 2006.
Ing. Anna Kuklíková, Ph.D., (*1954)
je absolventkou Fakulty stavební ČVUT v Praze, kde v současnosti působí jako pedagog. Během své dlouhé stavební praxe se podílela např. na rekonstrukci Národního divadla. Zabývá se vědecko-výzkumnou a normotvornou činností v oboru dřevěných konstrukcí, se zaměřením především na kompozitní dřevobetonové konstrukce. Je spoluautorkou řady vědeckovýzkumných a odborných publikací a norem.
Doc. Ing. Petr Kuklík, CSc., (*1949)
je absolventem Fakulty stavební ČVUT, kde v současnosti působí jako pedagog. Studijně pobýval na univerzitách a vědeckovýzkumných ústavech v Evropě, Austrálii, Japonsku a Kanadě. Zabývá se vědeckovýzkumnou a normotvornou činností v oboru dřevěných konstrukcí, a to jak na národní, tak mezinárodní úrovni. Je autorem a spoluautorem řady vědeckovýzkumných a odborných publikací a norem ISO, EN a ČSN. Je členem komisí mezinárodních organizací působících v oboru dřevěných konstrukcí – CEN, CIB, COST, ISO, IUFRO, RILEM.
