V letech 2008 a 2009 byl v rámci výzkumu a vývoje na Fakultě stavební Vysokého učení technického v Brně vyvinut systém kotvení předpínané FRP výztuže (informace byly mimo jiné publikovány i v Materiálech pro stavbu 2/2009). Vývoj systému dále pokračuje jak v rovině praktického používání (přípravky pro výrobu kotevních prvků přímo na stavbě, pro použití při dodatečném předpínání), tak v rovině teoretické.
Teoretický výzkum se soustředí především na zjištění vlivu rozměrů a počtu kotevních prvků na chování a únosnost kotevní oblasti a dále na odvození snadno použitelných návrhových vztahů, které by usnadnily použití předpínané FRP výztuže v praxi.
Důvod pro snahu o rozšíření používání předepnutých FRP výztuží je jednoznačný – jejich předepnutím lze mnohem lépe využít tahové vlastnosti kompozitních materiálů. Ty jsou schopny přenášet velké tahové síly, ovšem jejich relativně malý modul pružnosti (40 až 80 GPa v závislosti na použitých vláknech) může způsobovat problémy v chování betonových prvků s nepředepnutou FRP výztuží (větší deformace, rozvoj trhlin). Těmto problémům je možné předejít právě vnesením předpětí do výztuže.
Vzhledem k anizotropii materiálu kompozitu a z toho vyplývající nízké pevnosti v tlaku kolmo na vlákna je velice obtížné předepnutou výztuž konvenčními způsoby bezpečně zakotvit. Při použití standardních kotevních kuželíků s vroubkovaným povrchem vznikají v kotvené předpínané výztuži současně výrazné příčné stlačení, podélný smyk a osový tah. Tuto kombinaci vznikajících sil nelze ocelovými kotevními kuželíky do FRP výztuže bezpečně přenést, a proto celá řada výrobců modifikovala (případně zcela vyvinula) vlastní systém kotvení těchto výztuží (podrobněji viz např. [1], [2], [3]).
Na následujících řádcích je uveden pouze stručný výtah z analytického řešení daného problému. Text neobsahuje všechny teoretické předpoklady výpočtu a z nich odvozené závěry, jenž jsou uveřejněny v samostatném textu v teoretičtěji zaměřeném periodiku [8].
Princip působení nového kotevního prvku
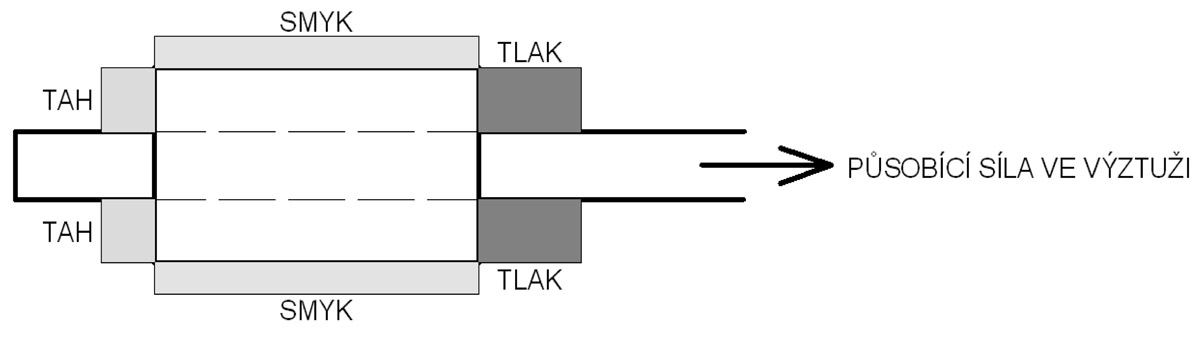
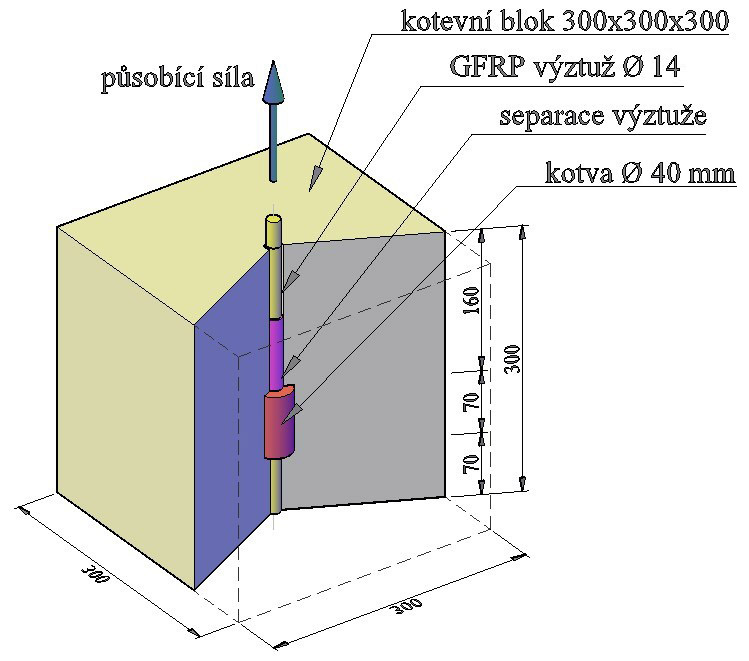
Vyvinutý kotevní systém [6] funguje na principu vytvoření dodatečné roznášecí plochy v kotevní oblasti výztuže, která umožňuje přenos předpínací síly z výztuže do okolního betonu na výrazně kratší vzdálenosti než při kotvení soudržností. Tato plocha je vytvořena nalepením jednoho nebo více válečků (tvořených ze speciální zálivky vyztužené vlákny) většího průměru na výztuž. Průměr válečku i jeho délka jsou variabilní. Celková únosnost vzniklé koncovky výztuže je dána kombinací smykové únosnosti povrchu kotevního prvku a otlačení jeho přední strany (obr. 1).
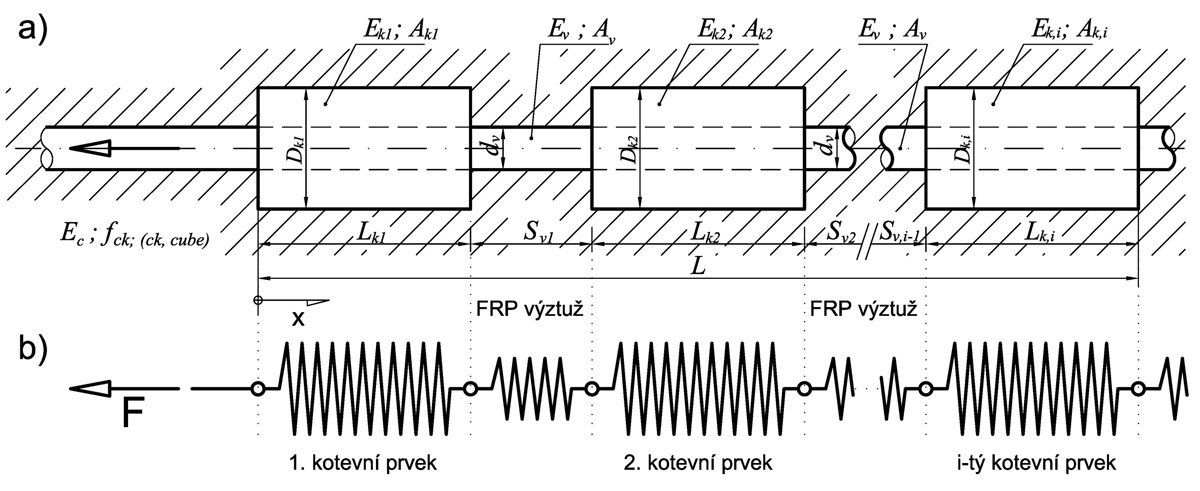
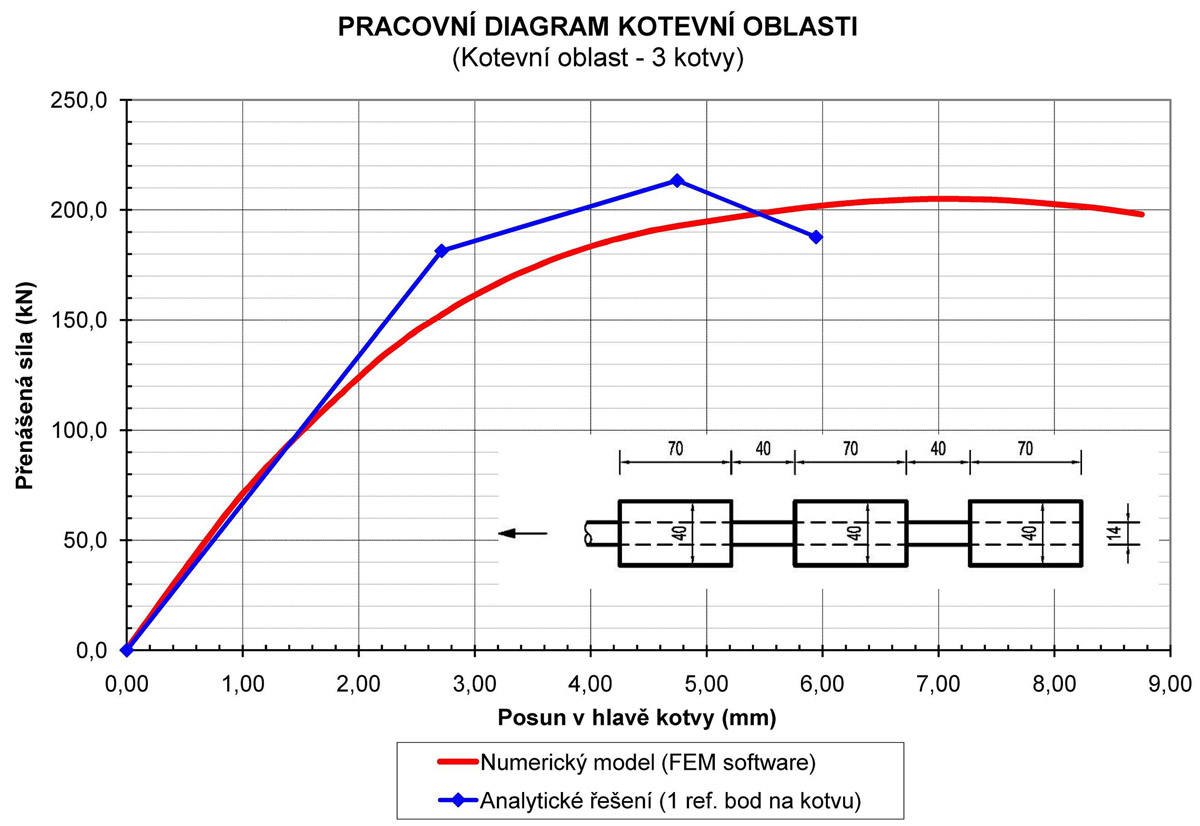
Kotevní prvky lze také kombinovat (kotvy lze na výztuži řadit do série, obr. 2), ať již pro zvýšení únosnosti či bezpečnosti kotevního systému, nebo pro snížení deformací v kotevní zóně (kotevní oblast je tužší).
Návrh kotevní oblasti
Návrh a posouzení kotevní oblasti vnitřních předpjatých FRP výztuží je důležitý z hlediska popisu závislosti vnášené předpínací síly na posunu kotvené výztuže. To následně umožňuje vyčíslení ztrát ve výztuži při jejím kotvení. Hlavní přenos sil, který má dominantní vliv na únosnost i deformace kotevního systému, probíhá v oblasti hlav jednotlivých kotev, jež tvoří „elastické zarážky“ prutu v betonu a působí jako pružiny opřené v hlavě o okolní beton. Působení kotevní oblasti lze proto popsat pomocí tuhostních parametrů jednotlivých komponent. Výsledné rovnice popisují závislost přenášené síly na posunu (přetvoření) jednotlivých míst kotevní oblasti, z čehož lze odvodit velikost ztráty v předpínané výztuži. Také je možno přidávat další prvky do kotevního systému (či upravovat parametry stávajících), aniž by se výrazně měnil postup výpočtu.
Kotevní systém lze idealizovat jako systém pružin řazených do série (obr. 2), které se společně podílejí na přenosu kotvené síly do okolního betonu. Při vnášení síly jsou postupně aktivovány jednotlivé pružiny a každá z nich odebírá sílu úměrnou její aktuální tuhosti. Celková únosnost je dána součtem sil, které přenesou čelní plochy (hlavy) lepených kotev v tlaku, a sil, které přenese tření mezi pláštěm kotvy a okolním betonem a tření mezi výztuží a okolním betonem; tah vznikající na konci (patě) kotvy (obr. 1) mezi betonem a kotvou lze zanedbat.
Celý kotevní systém je dle obr. 2 složen z:
● výztuže před hlavou první kotvy (dáno: plocha Av a modul pružnosti Ev);
● Nk kotevních prvků (dáno: plocha Ak, modul pružnosti Ek a délka kotvy Lki);
● Nk – 1 výztuží mezi kotevními prvky (dáno: Av, Ev, vzdálenost mezi kotevními prvky Svi).
Každý kotevní prvek i výztuž mezi kotvami lze rozdělit na n částí o délce elementu l (viz obr. 3).
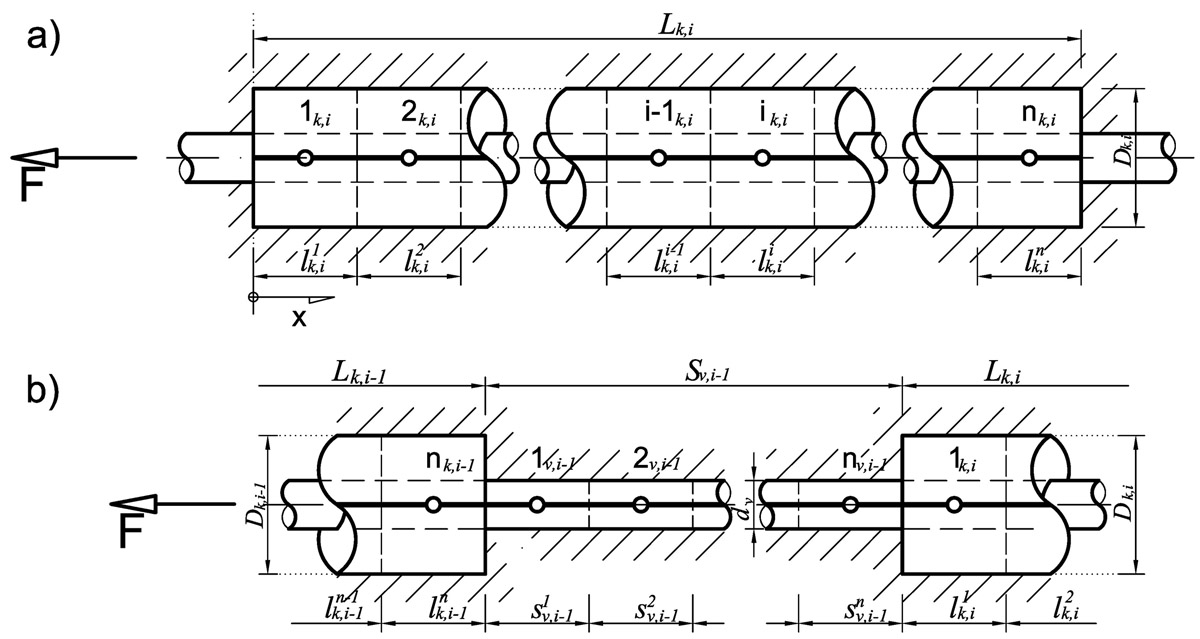
Jednotlivé dílčí elementy kotevního systému může v idealizovaném modelu představovat jeden referenční bod umístěný v těžišti elementu (tj. pro prutový prvek konstantního průřezu v polovině) a jemu příslušející neznámá deformace (posun). Na základě známých tuhostních parametrů jednotlivých komponent kotevního systému (tj. při znalosti Ev, Ek , Av a Ak) lze určit deformační stav v každém referenčním bodu kotvy.
Výslednou únosností kotevního systému je pak součet únosností všech jeho dílčích částí, tj. součet příspěvků kotev a výztuží mezi kotevními prvky:
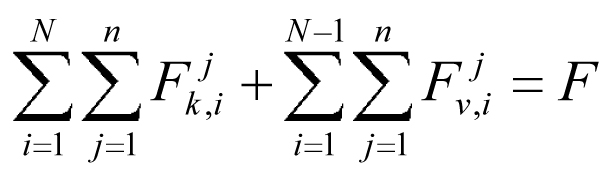 (1)
(1)kde je:
Fjk, i … únosnost j-tého elementu i-tého kotevního prvku;
Fjv, i … únosnost j-tého elementu i-té výztuže mezi kotevními prvky;
N … počet kotevních prvků v kotevním systému;
n … počet elementů kotevního prvku (výztuže mezi kotevními prvky).
Pro každou část kotevního systému (N kotevních prvků a N – 1 částí výztuží mezi prvky) o n dílčích elementech je sestaveno přesně n rovnic spojitosti, jež jsou modifikovány v závislosti na poloze řešených uzlů v kotevním systému. Ty jsou následně zařazeny do celkové (globální) matice podle polohy referenčních bodů v systému.
Výsledná soustava rovnic spojitosti obsahuje pouze n + 1 neznámých posunů u v jednotlivých referenčních bodech. Další hodnoty, které se v rovnicích vyskytují, jsou známy a chovají se jako konstanty. Dosazením konkrétní hodnoty za jeden neznámý parametr posunu (pro vykreslení pracovního diagramu je vhodné zvolit posun kontaktu výztuže v nultém bodu u0) bude v takto definované soustavě lineárních algebraických rovnic o n řádcích vystupovat přesně n neznámých. Tento systém lineárních rovnic, jenž má stejný počet rovnic jako neznámých, lze již jednoduše vyřešit.
Výsledkem je vždy exaktní (na bázi přijatých předpokladů) řešení pro konkrétní počáteční posun a tedy i stanovení odpovídajících posunů pro každý referenční bod oblasti. Z těchto posunů lze dopočítat hodnotu síly přenášenou v dané konfiguraci kotevní oblastí. Při opakované volbě počátečního posunu a následném řešení soustavy rovnic se získají jednotlivé body závislosti přenášené síly na posunu u0. Spojnice těchto bodů definuje pracovní diagram kotevní oblasti.
Teorie výpočtu kotevní oblasti umožňuje sestavit soustavu rovnic jak pro výpočet jednoho kotevního prvku, tak i pro soustavu dvou a více kotev. Do výpočtu je pouze nutno efektivně zahrnout část kotevního systému mezi jednotlivými kotvami (tj. tuhostní parametry výztuže). Samozřejmě je možno při výpočtu zavést zjednodušující předpoklady (například volbu pouze jednoho referenčního bodu na celou kotvu apod.), které mají rozdílný vliv na přesnost výsledného řešení. Je vždy nutno volit takový způsob výpočtu, který pro konkrétní případ dostatečně přesně vystihne skutečné chování kotevní oblasti.
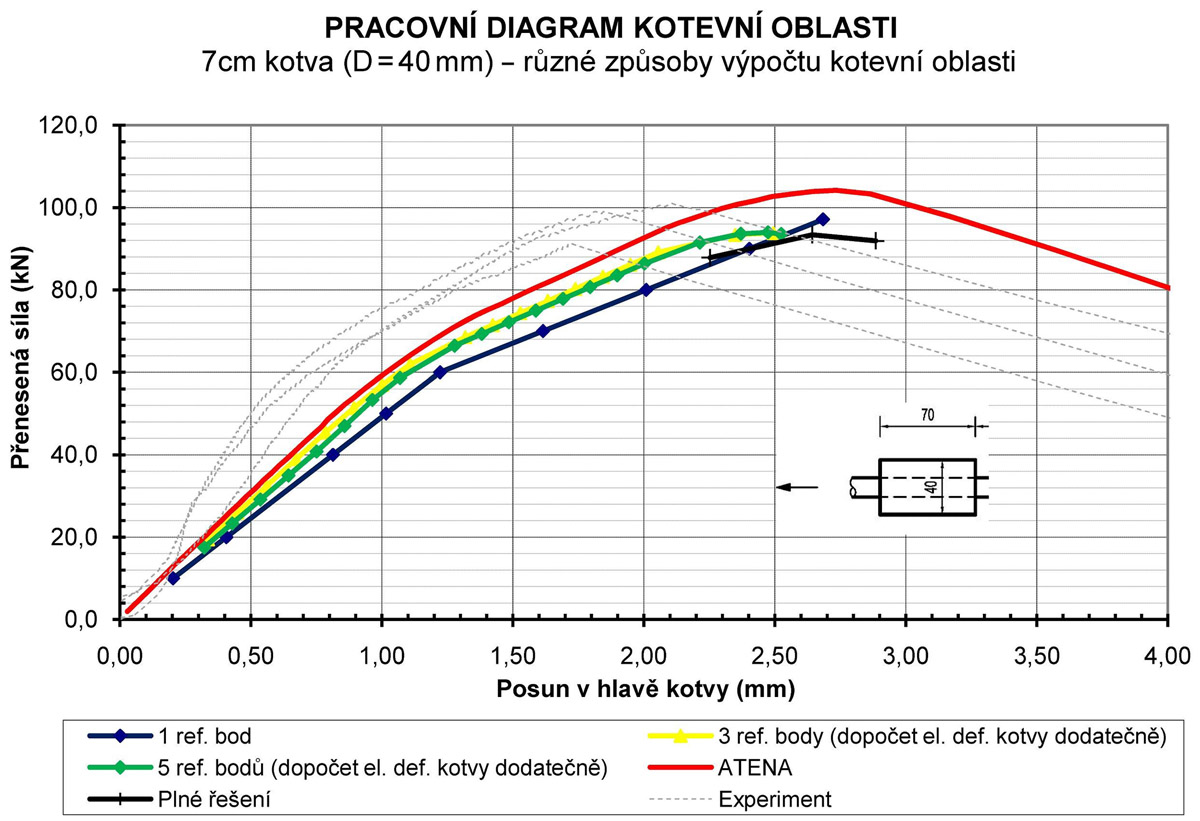 Na obr. 4 je uvedeno srovnání několika možných způsobů řešení kotevní oblasti pouze s jedním kotevním prvkem (průměr 40 mm, délka 70 mm, okolní beton C30/37). Zobrazen je nejjednodušší způsob výpočtu s jedním referenčním bodem pro celou kotvu (tj. sestavena pouze jedna deformační podmínka), výpočet pro počet elementů na jedné kotvě n = 3 a n = 5 za předpokladu tuhého chování kotevního válečku (jehož reálné elastické přetvoření je dopočteno až po určení posunů v kontaktu při předpokladu lineární změny průběhu síly na kotvě) a v neposlední řadě i plný výpočet bez zjednodušení pro n = 3 body. Graf je doplněn srovnáním s numerickým modelem a výsledky experimentálních měření na reálných vzorcích.
Na obr. 4 je uvedeno srovnání několika možných způsobů řešení kotevní oblasti pouze s jedním kotevním prvkem (průměr 40 mm, délka 70 mm, okolní beton C30/37). Zobrazen je nejjednodušší způsob výpočtu s jedním referenčním bodem pro celou kotvu (tj. sestavena pouze jedna deformační podmínka), výpočet pro počet elementů na jedné kotvě n = 3 a n = 5 za předpokladu tuhého chování kotevního válečku (jehož reálné elastické přetvoření je dopočteno až po určení posunů v kontaktu při předpokladu lineární změny průběhu síly na kotvě) a v neposlední řadě i plný výpočet bez zjednodušení pro n = 3 body. Graf je doplněn srovnáním s numerickým modelem a výsledky experimentálních měření na reálných vzorcích.Nachází-li se kotevní oblast v blízkosti okraje betonového prvku, je zřejmé, že výpočet již nelze provést dle předpokladů platných pro kotevní oblast v mase betonu a je nutno jej modifikovat. Ovšem výhodou zvoleného přístupu je, že stačí pouze upravit konstitutivní vztah popisující vlastnosti betonu a zohlednit vliv blízkého povrchu betonu prvku. Ten lze zohlednit např. stanovením jiné (nižší) tuhosti ve zhlaví kotvy a dosazením této hodnoty do výpočtu, který se jinak od předchozího neliší.
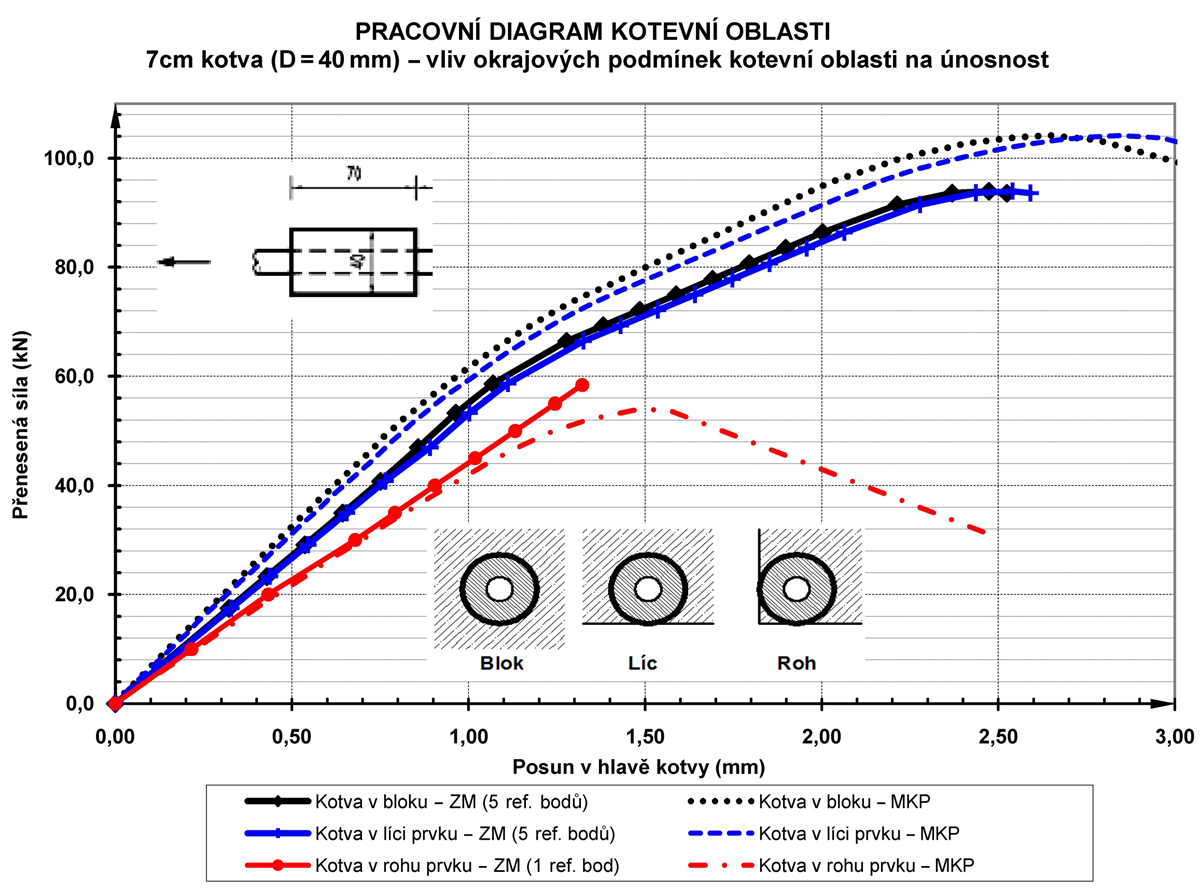 Z obr. 5 je patrné srovnání tří základních okrajových podmínek, jež při návrhu kotevní oblasti mohou nastat. Kotevní oblast je tvořena pouze jedním kotevním prvkem (průměr 40 mm a délka 70 mm, beton C30/37). Uveden je jak případ, kdy únosnost kotvy není ovlivněna okrajovými podmínkami (blok), tak i situace, kdy již dochází k ovlivnění (snížení) únosnosti systému okrajem prvku (líc, roh). Pro všechny tři limitní případy je zobrazeno i srovnání s výsledky dosaženými výpočtem MKP v programu ATENA.
Z obr. 5 je patrné srovnání tří základních okrajových podmínek, jež při návrhu kotevní oblasti mohou nastat. Kotevní oblast je tvořena pouze jedním kotevním prvkem (průměr 40 mm a délka 70 mm, beton C30/37). Uveden je jak případ, kdy únosnost kotvy není ovlivněna okrajovými podmínkami (blok), tak i situace, kdy již dochází k ovlivnění (snížení) únosnosti systému okrajem prvku (líc, roh). Pro všechny tři limitní případy je zobrazeno i srovnání s výsledky dosaženými výpočtem MKP v programu ATENA.Při návrhu kotevní oblasti je také velmi důležité omezit hodnotu maximálního posunu výztuže na počátku první kotvy z hlediska mezního stavu použitelnosti. Přesná hodnota musí být určena přímo pro navrhovaný prvek, neboť vždy záleží na rozponu prvku a na působícím zatížení. Je nutno respektovat maximální dovolené průhyby dle [5] a zároveň navrhnout kotevní oblast tak, aby nedocházelo vlivem posunu výztuže v kontaktu (který se do výpočtu prvku promítá analogicky jako ztráta pokluzem) k velkým ztrátám předpětí.

 Závěr
ZávěrVyvinutý systém kotvení zachovává veškeré výhody FRP výztuží – neobsahuje žádné kovové části. Proto je možné aplikovat ho na všechny speciální případy, které vyžadují právě použití nekovových výztuží.
Výše popsané analytické řešení kotevních oblastí vykazuje dobrou shodu s provedenými experimenty a numerickými studiemi. Pro plné ověření správnosti odvozených vztahů a celkového přístupu k řešení problému je však nutno provést další experimenty, které mají za úkol ověřit především chování skupiny kotev, a to jak jejich působení v mase betonu, tak i u okraje. Nové výsledky získané z těchto experimentů budou odborné veřejnosti prezentovány v průběhu následujících měsíců.
FRANTIŠEK GIRGLE, DAVID HORÁK, PETR ŠTĚPÁNEK
foto archiv autorů
Prezentované výsledky výzkumu byly získány za finanční podpory projektu MPO TIP FR-TI1/357 Betonové konstrukce s nekovovou výztuží se zvýšenou požární odolností a odolností vůči agresivním vlivům a projektu MŠMT 1M0579 v rámci činnosti výzkumného centra CIDEAS a projektu GAČR P104/10/2153 Kompozitní konstrukce na bázi vysokohodnotných silikátů a dřeva – environmentální optimalizace a experimentální ověření.
Literatura:
1) Vistasp, M. Karghari: Use of composite Materials in civil infrastructure in Japan. Baltimore, Maryland, 1998.
2) Erki, M. A. – Rizkalla, S. H.: Anchorage for FRP reinforcement. Concrete international 1993.
3) Horvatits, J. – Benko, V. – Kollegger, J.: První použití externích předpínacích kabelů z uhlíkových vláken na zesílení mostu v Rakousku. BETON TKS, 4/2006.
4) Štěpánek, P. – Horák, D. – Prokeš, J.: New prestressing system for FRP reinforcement in concrete structures. Příspěvek na konferenci 9th International Symposium on Fiber-Reinforced Polymer Reinforcement for Concrete Structures, Sydney, The University of Adelaide, 2009.
5) ČSN EN 1992-1-1 (73 1201) Navrhování betonových konstrukcí. Část 1-1: Obecná pravidla a pravidla pro pozemní stavby. ČNI 2006.
6) Patentová přihláška číslo 2008-475.
7) Horák, D. – Štěpánek, P.: Vývoj nekovových výztuží 2. Materiály pro stavbu 2/2009.
8) Girgle, F. – Štěpánek, P. – Horák, D. – Ďurech, D. – Laníková, I.: Systém kotvení předpjaté FRP výztuže. Stavební obzor 2/2011.
Ing. František Girgle (*1983)
absolvoval VUT FAST v Brně, kde v současnosti působí na ústavu betonových a zděných konstrukcí jako výzkumný a akademický pracovník. Jeho hlavní specializací je navrhování odolných konstrukcí vyztužených převážně vnitřní nekovovou výztuží.
Ing. David Horák (*1980)
absolvoval VUT FAST v Brně, kde v současnosti působí na ústavu betonových a zděných konstrukcí jako výzkumný pracovník. Jeho hlavní specializací je vyztužování a zesilování konstrukcí nekovovými materiály.
Prof. RNDr. Ing. Petr Štěpánek, CSc., (*1953)
absolvoval FAST VUT v Brně a PřF UJEP Brno – nyní Masarykova univerzita. Je autorizovaným inženýrem pro obor statika a dynamika. Pracoval jako statik v Keramoprojektu Brno. Je prorektorem pro strategický rozvoj VUT v Brně a vedoucím ústavu betonových a zděných konstrukcí na Fakultě stavební.








