Tento článek ozřejmuje, do jaké míry jsou difuzních fólie vodotěsné, jsou-li vystaveny dešti. Podstřešní fólie se používají jako pojistné hydroizolační vrstvy v odvětrávaných šikmých střechách. Podkrovní prostory chrání před prachem a vlhkostí z deště a sněhu, které se mohou dostat pod skládanou krytinu, dále před vodou kondenzující na spodním líci nenasákavé krytiny a v neposlední řadě chrání před vlhkostí pronikající při destrukci střešní krytiny. U půdních vestaveb navíc chrání tepelnou izolaci proti vlhkosti. Používají se u dvouplášťových i tříplášťových střech.
Difuzní fólie tvořící funkční vrstvu pojistné hydroizolace v konstrukcích šikmých střech urazily za posledních 25 let mimořádně dlouhou cestu nejen ve svém vývoji, ale i v samotné realizaci na stavbách. Místo výlučně polyetylenových fólií s mikroperforací, které mohly být aplikovány pouze ve tříplášťových skladbách střešních konstrukcí, dnešní trh nabízí neuvěřitelnou škálu difuzních fólií, které mají řadu speciálních technických vlastností, umožňujících řešení pojistné hydroizolace libovolné konstrukce šikmé střechy.
Tak najdeme fólie s extrémně vysokými pevnostními parametry, fólie výrazně omezující úniky tepla díky svým reflexním vlastnostem a neposlední v řadě i takové produkty, které jsou zcela rezistentní vůči prostředkům preventivní ochrany dřeva.
Nicméně základní vlastnost, vodonepropustnost, zůstává i nadále tím základním důvodem, proč jsou obecně navrhovány, zejména v případech, kdy je svrchní střešní plášť tvořen skládanou krytinou. Je třeba připustit zcela legitimní vlastnost skládaných krytin, že nejsou těsné proti polétavému sněhu a tlakové vodě. V českých klimatických podmínkách lze riziko zafoukání sněhu rozumně předpokládat nejenom spárami mezi prvky krytiny, ale (a to zejména) v oblasti napojení prostupů na krytinu. Míra průniku sněhu je závislá nejen na klimatických podmínkách, ale i na orientaci střešní konstrukce, tvaru střechy v závislosti na konfiguraci terénu, složitosti střechy apod. Nicméně je to i pokrývač, který může do značné míry ovlivnit, kolik sněhu pronikne do podstřeší.
Vraťme se však k základní vlastnosti – k nepropustnosti. Kdyby totiž tyto fólie nebyly vodonepropustné, pak by ztratily v technické praxi svůj smysl. A přece jen můžou existovat určité podmínky, samozřejmě jen časově omezené, kdy to, co dělá z fólie pojistnou hydroizolaci, selhává. Je to dynamický ráz dešťových kapek v době, kdy je fólie přímo (tj. bez krytiny) vystavena povětrnostním vlivům. Zkusme se na tuto situaci podívat zblízka.
Dopadová rychlost a energie dešťové kapky
Při pádu dešťové kapky na ni působí dvě síly: tíha G a odpor vzduchu F. Čím je větší rychlost pádu, tím (se čtvercem rychlosti) roste odpor vzduchu, až dojde k vyrovnání obou sil a od toho okamžiku padá kapka konstantní rychlostí (tzv. terminální rychlost pádu, která je maximálně možná).
Tíha
G = m · g,
kde
m … hmotnost kapky,
g … zemské zrychlení.
Odpor vzduchu
F = 1/2 S . cw ρa c²,
kde
S … plocha průmětu kapky kolmá na směr pádu,
cw … součinitel odporu prostředí,
ρa … měrná hmotnost prostředí (vzduchu)
c …dopadová rychlost.
Při rovnováze G = F platí:
4/3 π . r³ . ρh . g = 1/2 π . r² . cw . ρa . c (1)
Dopadovou rychlost lze vypočítat podle vztahu:
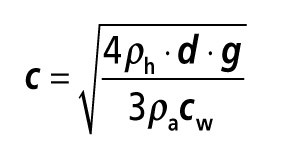 (2),
(2),kde
ρh … je měrná hmotnost vody (1000 kg/m³),
d … je průměr dešťové kapky (200 až 2500 μm),
ρa … je měrná hmotnost vzduchu (cca 1,25 kg/m³),
cw … je součinitel aerodynamického odporu vzduchu (pro kouli 0,5),
g … je zemské zrychlení 9,81 m/s².
Do rovnice (1) se průměr dešťové kapky dosazuje pochopitelně v [m]. Dosazením známých hodnot a dosazením průměru dešťové kapky v [mm] se rovnice (2) zjednoduší na:
c = 4,57 . √d (3)
Při průměru kapky např. 1 mm je dopadová rychlost c = 4,57 m/s.
Poznámka:
Dešťové kapky mají zpočátku kulovitý tvar, avšak při pádu vlivem odporu vzduchu se jejich tvar na spodní straně zplošťuje, až může mít kapka spodní stranu vydutou. To platí pro kapky o větším počátečním průměru. V důsledku vydutí dojde ke snížení povrchového napětí a kapka se roztříští na x menších kapek. Tyto malé kapičky však v důsledku setrvačnosti mají i mnohem větší dopadovou rychlost než by vyšlo podle (3).
Pro výpočet kinetické energie při dopadu dešťové kapky se použije rovnice:
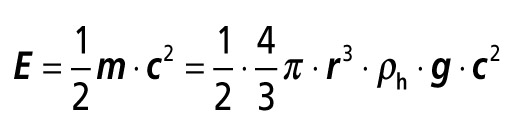 (4)
(4)z níž má dešťová kapka o průměru 1 mm energii E = 53,6.10–6 J.
V případě, že naprší za 5 min na plochu 1 m² 10 litrů dešťové vody, pak ze vztahu:
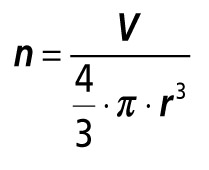 (5)
(5)vypočítáme počet dešťových kapek n = 19,1 . 106 s celkovou kinetickou energií E = 1023 J.
Pokud by však průměr kapek byl 2,5 mm, pak by při napršeném množství 10 litrů činila celková kinetická energie již 25,7 kJ.
Nás však zajímá vyjádření dynamického rázu při dopadu dešťové kapky na difuzní fólii ve stavu, kdy je položena fólie, avšak střecha je zatím bez krytiny, jinou veličinou, a sice výškou vodního sloupce h. Úpravou Bernoulliovy rovnice dostaneme
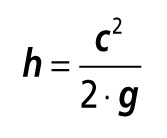 (6)
(6)Při dopadu dešťové kapky o průměru 1 mm lze zatížení fólie přirovnat k zatížení výškou vodního sloupce 1,06 m, avšak při dopadu kapky o průměru 2,5 mm již je výška vodního sloupce působícího na fólii 2,66 m.
Poznámka:
Odolnost difuzních fólií proti průsaku dešťové vody se udává hydrostatickým zatížením vodním sloupcem o výšce např. 3 m. Není bez zajímavosti, že toto zatížení odpovídá dynamickému rázu dešťové kapky o průměru 2,8 mm, tedy nepatrně větší než výše uvedená hodnota. Během prudkého letního deště však mohou být kapky i mnohem větší, 5 mm i více. V roce 2004 byly zaznamenány na Marshallových ostrovech dešťové kapky o průměru 10 mm! Je tedy zřejmé, že v extrémních případech, kdy na nezakrytou fólii dopadají kapky o velikosti větší jak 2,8 mm, může dojít k průsaku vody fólií.
Tabulka: Výška vodního sloupce h v závislosti na průměru dešťové kapky d
|
d [mm]
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
h [m]
|
1,07
|
2,13
|
3,2
|
4,27
|
5,33
|
6,4
|
7,47
|
Poznámka: Stejné vztahy platí i pro výpočet dopadové rychlosti a energie tuhého hydrometeoru, jakým je třeba kroupa. V případě kroupy bude rovnice (3) ve tvaru c = 4,39 d0,5, kde d je v [mm].
Ve výše uvedených úvahách jsem zanedbal vztlakovou sílu vyplývající z objemu padajícího tělesa, neboť měrná hustota vzduchu je nepatrná.
Dopadová rychlost na šikmou střechu za větru
Výše uvedené úvahy a výpočty platí za předpokladu, že směr vektoru rychlosti je kolmý k rovině dopadu dešťové kapky. Vzhledem k tomu, že se v tomto pojednání zabývám šikmými střechami, nemusí být tento předpoklad vždy splněn a také zpravidla ani nebývá. Zároveň je třeba vzít v úvahu odklon vektoru rychlosti dešťové kapky působením větru, viz obr. 1 a 2.
Za bezvětří je vektor rychlosti c0 kolmý k vodorovné rovině, a proto se rozkládá na dvě složky: rovnoběžnou s rovinou střechy ct a kolmou na rovinu střechy cn. Mají-li obě střešní roviny stejný sklon, pak složka cn je stejně veliká na obou střešních plochách podle rovnice:
cn = c0 . cos α (7).
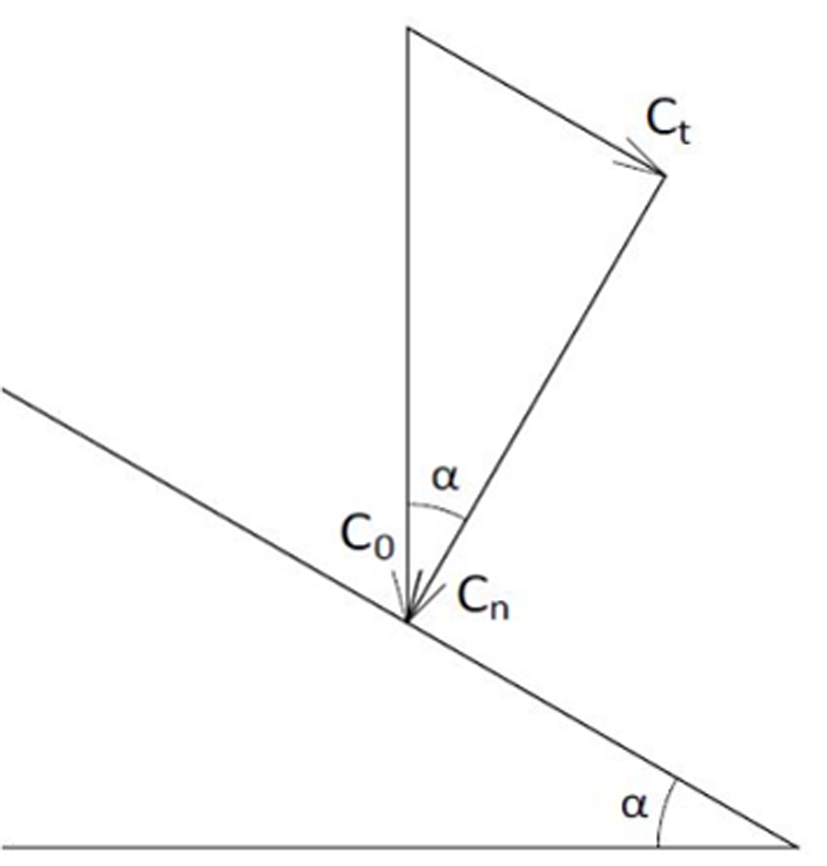
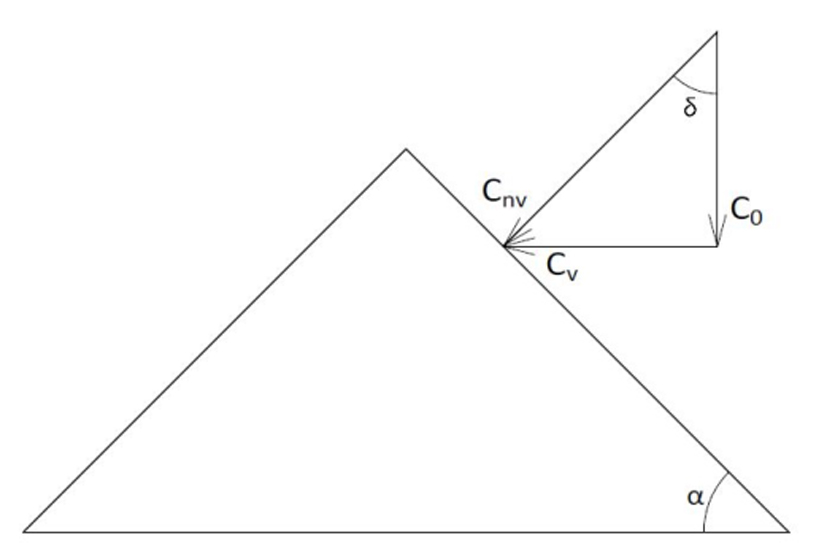
Při současném působení větru se však trajektorie dešťové kapky odchyluje ze svislé roviny o úhel δ, jehož velikost závisí na rychlosti větru. A tak může nastat situace, že dopadová rychlost dešťové kapky na návětrné střešní ploše cnv bude výslednicí rychlosti c0 a rychlosti větru cv se směrem kolmým na střešní rovinu, a tedy i mnohem větší než za bezvětří. Na závětrné straně bude však velikost vektoru cn nulová.
Příklad:
Dešťová kapka o průměru pouhý 1 mm je unášena větrem o rychlosti cv = 80 km/h (22,2 m/s). Z Pythagorovy věty dostaneme výslednou rychlost kolmou na rovinu střechy:
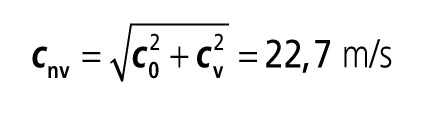 (8)
(8)Dosazením této hodnoty do rovnice (6) zjistíme, že tato dopadová rychlost už působí na fólii na návětrné straně jako vodní sloupec vysoký 26,2 m!
Závěrem
Z příkladu se zdá na jednu stranu nepochybné, že běžně deklarovaná vodotěsnost difuzních fólií výškou vodního sloupce cca 3 m již příliš důvěry nedává. Z praxe jsou známy případy, kdy na jedné střešní ploše došlo k masivnímu průsaku vody fólií, zatímco na druhé střešní ploše žádný průsak zjištěn nebyl.
Na druhé straně je však třeba nahlížet na podobné situace realisticky. Je-li odebrán vzorek difuzní fólie k laboratornímu testu na vodonepropustnost a není-li na něm shledána žádná vada, pak si je třeba uvědomit jednu zásadní skutečnost: Difuzní fólie neslouží jako nouzové zakrytí, difuzní fólie není dimenzována na zatížení deštěm jako krytina, je to pouze pojistná hydroizolace. Nic více, a nic méně. Nedávný případ výše uvedené jen potvrzuje. Na sever orientovaná střešní plocha vykazovala masivní průsak, jižní byla bez problémů. Za poměrně silného deště vál silný severní vítr. Po zakrytí střechy vlastní krytinou se již nikdy nemůže podobná situace opakovat.
I když meteorologické statistiky vykazují relativně malou současnost silného deště a silného větru, nelze tuto současnost vyloučit. Naposledy to bylo v noci z 15. na 16. srpna 2010, kdy vichřice vyvracela stromy a současně docházelo k místním záplavám.
Závěrečná poznámka:
Výše uvedené úvahy jsou založeny na zjednodušeném předpokladu, že dopadová plocha je tuhá deska, tj. že veškerá kinetická energie se přemění v odpovídající zatížení vodním sloupcem. Tomuto předpokladu se v praxi blíží situace, kdy je fólie položená na bednění, i když i v tomto případě je třeba připustit jistou míru pružnosti podkladního bednění. V případě, že je fólie volně natažená na krokvích či je položená na tepelné izolaci, je pochopitelné, že útlum dynamického rázu při dopadu dešťové kapky na fólii bude větší.
Další vliv na průsak dešťové vody nezakrytou fólií má aplikace prostředků preventivní ochrany dřeva, což je obecně známý fenomén, jemuž je možné blíže se věnovat v některém z dalších čísel časopisu Materiály.
MILAN HOLEC
Ing. Milan Holec (*1946)
byl po absolvování ČVUT Praha zaměstnán v různých průmyslových podnicích převážně se stavební orientací. V současné době pracuje ve firmě Bramac střešní systémy, spol. s r. o., jako vedoucí oddělení technických expertíz.











