Porovnanie vplyvu kotvenia zábradlí z vrstveného skla

Zábradlia z vrstveného bezpečnostného skla bez stĺpikov a madiel sú architektonicky zaujímavé a vo veľkej miere obľúbené. Problém nastáva pri voľbe a návrhu upevnenia zábradlia ku konštrukcii. Existuje veľa spôsobov uchytenia zábradlí zo skla, z ktorých som vybral niekoľko druhov a porovnal ich vplyv na zaťaženie skla.

V súčasnosti je sklo v stavebníctve veľmi rozšíreným materiálom. Čoraz častejšie nahrádza iné materiály vo funkcii nosného prvku, ktorý prenáša zaťaženie nielen od vlastnej tiaže, ale aj od premenných zaťažení, ako sú vietor, sneh a dokonca pohyb osôb. 

Zábradlia zo skla sú v dnešnej dobe obľúbeným prvkom v obchodných centrách, bytových domoch a pod. V článku sa zaoberám zábradliami bez stĺpikov a madiel. Je veľa možností ukotvenia sklených tabúľ, napríklad líniové (obr. 1a), bodové (obr. 1b, c), pásikové (obr. 2b) a rôzne iné. Hlavne by som ich rozdelil na sklené tabule s dierami a bez dier, kde diery výrazne oslabujú sklený prvok.

Modelovanie a numerická analýza

Úloha a ciele modelovej štúdie 
Úlohou štúdie bolo analyzovať interiérové zábradlie z vrstveného kaleného skla s rôznym spôsobom kotvenia pri normovom krátkodobom zaťažení vo vodorovnom smere. Z dôvodu zjednodušenia je zvolené interiérové zábradlie – nepočítame s účinkami vetra a materiálovými charakteristikami pre PVB fóliu (pri izbovej teplote 20 °C). Všetky typy zábradlí boli navrhnuté tak, aby ich výška nad úrovňou podlahy (1100 mm) a šírka sklenej tabule (1200 mm) bola rovnaká. Cieľom štúdie bolo zistiť skutočné správanie tabúľ vrstveného skla, posúdiť ich a nájsť najvýhodnejšie a najnevýhodnejšie kotvenie skleného zábradlia.

Metódy riešenia 
Riešenie úlohy bolo realizované programom ANSYS, ktorý pracuje na princípe metódy konečných prvkov (MKP). Pre riešenie zvolenej problematiky bol zvolený typ elementov pre objemy SOLID187 (SOLID92). Model bol riešený v 3D.

Keďže model obsahuje len izotropné mate-riály, mechanické vlastnosti boli definované prostredníctvom Youngovho modulu pružnosti E, Poissonovej konštanty priečneho pretvorenia µ a hustoty použitých materiálov ρ. Materiálové charakteristiky pre PVB fóliu boli odčítané z grafu [5] pre teplotu okolitého prostredia 20 °C a dobu trvania zaťaženia 5 sekúnd.

Použité výpočtové modely 
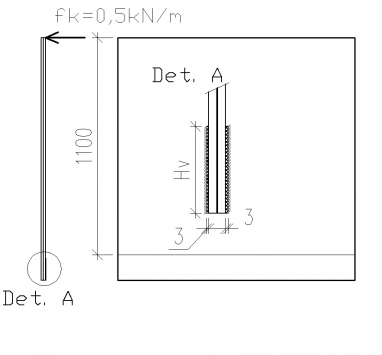
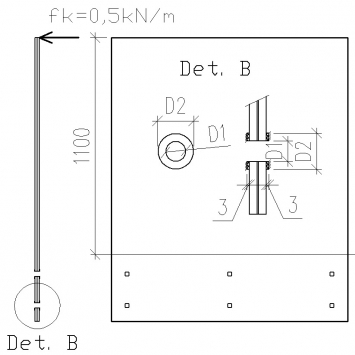
Spolu bolo namodelovaných 28 modelov v programe ANSYS s rôznymi spôsobmi kotvenia sklených tabúľ. Všetky modely boli modelované s rovnakou hrúbkou sklených tabúľ 15 mm a PVB fólie 1,52 mm, teda vrstvené sklo zložené zo sklenej tabuľe + PVB fólie + sklenej tabuľe (15 mm + 1,52 mm + 15 mm). Podľa [6], tabuľky 6.12 – Vodorovné zaťaženia priečok a parapetov je pre kategóriu A, B a C1 (A – Plochy pre domáce aktivity a obytné účely, B – Administratívne plochy, C1 – Plochy so stolmi atď.) odporúčaná charakteristická hodnota priamkového zaťaženia q_k = 0,5 kN/m v horizontálnom smere a toto zaťaženie bolo modelované na hornej hrane sklenej tabule (charakteristická hodnota pre výpočet priehybov a návrhová pre výpočet napätí) [5]. Kotvenie na všetkých modeloch je riešené cez gumené pásy na oboch stranách tabule o hrúbke 3 mm, ktoré je pevne spojené z jednej strany so sklom a z druhej strany sú neposuvné plošné okrajové podmienky (obr. 3a, b). Odsadenie dier od okraja sklených tabúľ je 80 mm, priemer diery v sklených tabuliach je D₁ = 26 mm a priemer kotviacich gumených podložiek je D₂ = 46 mm.

Na obrázku 4 sú znázornené nasledovné spôsoby kotvenia skleného zábradlia: a) líniové H_v = 80, 110, 120 mm, b) líniové s jednou radou skrutiek, c) líniové s dvomi radmi skrutiek, d) pásikové bez dier v skle, šírka pásika je 40 mm, e) pásikové s dierami v skle, šírka pásika je 40 mm, odsadenie diery od horného okraja pásika je 30 mm, f) bodové s jednou radou, g) bodové s dvomi radmi v = 80, 160, 180, 200 mm.

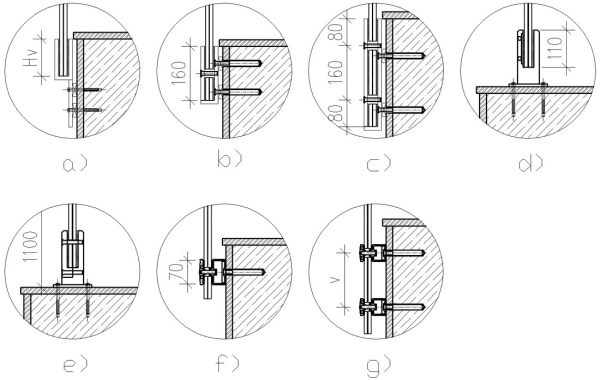
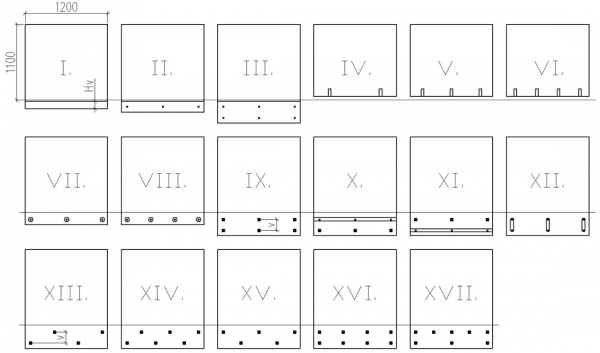
Na obrázku 5 sú znázornené schémy sklených zábradlí s rôznymi spôsobmi kotvenia a ich rozmiestnenia. 

Výsledky numerickej analýzy 
Výsledné napätia a priehyby z numerickej analýzy sú uvedené v tabuľke č. 3. Vypočítaná návrhová pevnosť kaleného skla v ťahu podľa normy [7] je 50 MPa. Medzná hodnota vodorovného priehybu zábradlia z vrstveného skla nie je definovaná v normách, a teda v praxi si limitný priehyb stanovuje investor. Podľa normy STN EN 1993-1-1 pre priečle zasklenia je medzná hodnota vodorovných priehybov L/200, teda v tomto prípade 6 mm [8].

Tabuľka 1: Materiálové charakteristiky zadávané do programu ANSYS

Tabuľka 2: Výsledné ťahové napätia (hlavné σ₁, σ₂ a normálové napätia σ_x, σ_y) a priehyby pre sklenené zábradlia s rôznymi spôsobmi kotvenia sklených tabúľ

Záver 
Namodelovaných bolo 28 modelov zábradlia z vrstveného kaleného skla v programe ANSYS s rôznymi spôsobmi kotvenia. Na základe získaných výsledkov numerickej analýzy vyplýva, že veľmi záleží na spôsobe uchytenia zábradlia, aj keď ide o rovnakú hrúbku, šírku, zaťaženie a výšky nad úrovňou podlahy. Na návrhovú pevnosť kaleného skla v ťahu vyhovelo 17 modelov. 

Najvýhodnejšie z hľadiska ťahových napätí z numerickej metódy vyšli modely: 5) líniové uloženie s dvomi radmi skrutiek, 4) s jednou radou skrutiek, 3) líniové s výškou votknutia H_v = 120 mm atď. Naopak najnevýhodnejšie z hľadiska ťahových napätí vyšli modely od najhoršieho: 24) s bodovým kotvením s dvomi radmi po dvoch úchytoch, posunutými, v = 80 mm, 23) s bodovým kotvením s dvomi radmi po dvoch úchytoch, posunutými, v = 160 mm, 9) pásikové s dvomi úchytmi s dierami atď. 

Potvrdilo sa, že otvory výrazne oslabujú sklenú tabuľu, čo má vplyv na ťahové napätia, ale nemá vplyv na priehyb. Špičky ťahových napätí sa nachádzajú priamo v otvoroch (obr. 6). Rozdiel napätí na zábradliach bez dier a s dierami na skrutky je preukázané na modeloch č. 6, 7, 8 (s pásikovým kotvením s 2, 3, 4 úchytmi bez dier) a modeloch č. 9, 10, 11 (s pásikovým kotvením s 2, 3, 4 úchytmi s dierami). Rozdiel ťahových napätí medzi modelmi bez dier a s dierami sa pohybujú až okolo 20 MPa, čo je rozhodujúce pri návrhovej odolnosti skla v ťahu. 

Pri daných vstupných parametroch vyhoveli všetky modely na návrhovú pevnosť v ťahu u líniovo uložených zábradliach. Modely s pásikovým kotvením bez dier sú výhodné z hľadiska nižšej celkovej výšky sklenej tabule a jednoduchého uchytenia, ale pri tabuli s dvomi úchytmi je potrebné zakotviť vrchnú časť tabule z dôvodu zabezpečenia proti priehybu. Pásikové kotvenie s dierami odporúčam pri daných parametroch až so štyrmi úchytmi. V prípade bodového kotvenia s jednou radou vyhovel model so štyrmi úchytmi s D₂ = 70 mm, kde je taktiež potrebné zamedzenie priehybu sklenej tabule. Pri bodových kotveniach s dvomi radmi úchytov odporúčam po troch úchytoch s väčšou zvislou vzdialenosťou ako v = 180 mm, alebo D₂ = 70 mm, alebo D₁ = 36 mm. Analýza ďalej ukázala, že zmenšenie priemeru diery z 26 mm na D₁ = 16 mm má nepriaznivý vplyv, ale naopak zväčšenie diery na D₁ = 36 mm sa ukázalo ako pozitívne. Zvislé roznášacie platne v modeli 22) sa ukázali ako neúčinné, znížil sa priehyb iba o 2 mm. 

Priehyby pri viacerých modeloch vyšli nevyhovujúco veľké a psychologicky by zle vplývali na ľudí. V praxi sa tieto priehyby sklených zábradlí eliminujú kovovými madlami vo vrchnej časti sklenej tabule, ktoré sa prípadne môžu kotviť do steny. Na priehyb vyhoveli iba dva modely, a to s líniovým uložením s dvomi radmi skrutiek a s jednou radou skrutiek a môžem povedať že aj líniové uloženie s výškou votknutia H_v = 120 mm a H_v = 110 mm. Pri ostatných modeloch by bolo nutné kotviť sklené tabule vo vrchnej časti do okolitých stien alebo konštrukcií.

Poďakovanie 
V článku sú prezentované výsledky z projektu NSF POS, ktorý vznikol za podpory Programu na podporu mladých výskumníkov 2014. 

ĽUBOŠ BALCIERÁK
foto archiv firem Metalinox, s. r .o., (1) a  Trescalini (2)

Literatúra:
1) www.metalinox.sk.
2) www.stilmetal.net.
3) www.trescalini.fr.
4) www.spaceup.sk.
5) SOBEK, W., M. KUTTERER, R. MESSMER. Rheo-logisches Verhalten von Schubverbund, Forschungsbericht. Universität Stuttgart, 1998.
6) STN EN 1991-1-1 Zaťaženie konštrukcií. Časť 1-1: Všeobecné zaťaženia – Objemová tiaž, vlastná tiaž a úžitkové zaťaženie budov, Tabuľka 6.12 – Vodorovné zaťaženia priečok a parapetov, s. 23.
7) DIN EN 13474-1 Glas im Bauwesen – Bemessung von Glasscheibgen – Teil 1: Allgemeine Grundlagen für Entwurf, Berechnung und Bemessung.
8) STN EN 1993-1-1 Navrhovanie oceľových konštrukcií. Časť 1-1: Všeobecné pravidla a pravidla pre budovy, NA.2.23 Článok 7.2.2(1)B Vodorovné priehyby, poznámka B.

Ing. Ľuboš Balcierák (*1988)
absolvoval obor konstrukce a dopravní stavby na Stavební fakultě Slovenská technické univerzity v Bratislavě, kde v současnosti studuje doktorandské studium. Zároveň pracuje jako pomocný projektant v útvaru nerezových konstrukcí ve firmě INGSTEEL, spol. s r. o.